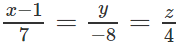Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Giải SBT Toán 12 Bài 3: Phương trình đường thẳng !!
Viết phương trình của đường thẳng denta nằm trong mặt...
Viết phương trình của đường thẳng denta nằm trong mặt phẳng (alpha): x + 2z = 0
Câu hỏi :
Viết phương trình của đường thẳng nằm trong mặt phẳng (): x + 2z = 0 và cắt hai đường kính
* Đáp án
* Hướng dẫn giải
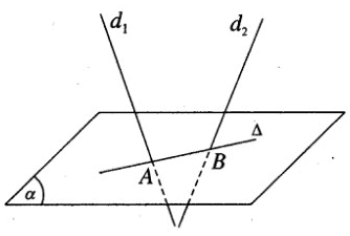
Gọi A và B lần lượt là giao điểm của và với (α). Đường thẳng cần tìm chính là đường thẳng AB.
Ta có: A(1 − t; t; 4t)
A () ⇔ t + 4.(2t) = 0 ⇔ t = 0
Suy ra: A(1; 0; 0)
Ta có : B(2 − t′; 4 + 2t′; 4)
B () ⇔ 4 +2t′ + 8 = 0 ⇔ t′ = −6
Suy ra B(8; -8; 4)
đi qua A, B nên có vecto chỉ phương = (7; −8; 4)
Phương trình chính tắc của là:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 12 Bài 3: Phương trình đường thẳng !!
Số câu hỏi: 27
Copyright © 2021 HOCTAP247