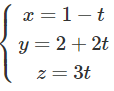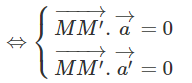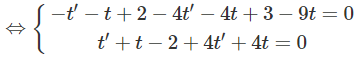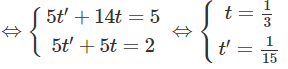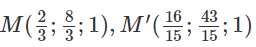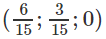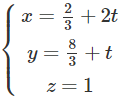Cho hai đường thẳng: d: (x - 1)/-1 = (y - 2)/2 = z/3 và d': x = 1 + t' y = 3 - 2t' z = 1

* Hướng dẫn giải

Phương trình tham số của đường thẳng d: 

Vecto chỉ phương của hai đường thẳng d và d’lần lượt là $\overrightarrow{\mathrm{a}}$ = (−1; 2; 3), $\overrightarrow{\mathrm{a}\text{'}}$ = (1; −2; 0).

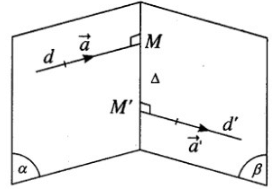
Xét điểm M(1 – t; 2 + 2t; 3t) trên d và điểm M’(1 + t’; 3 – 2t’; 1) trên d’ ta có $\overrightarrow{\mathrm{MM}\text{'}}$ = (t′ + t; 1 − 2t′ − 2t; 1 − 3t).

MM’ là đường vuông góc chung của d và d’.

Thay giá trị của t và t’ vào ta được tọa độ M và M’ là

Do đó MM'→ = 

Suy ra đường vuông góc chung Δ của d và d’ có vecto chỉ phương $\overrightarrow{\mathrm{u}}$ = (2; 1; 0)

Vậy phương trình tham số của $∆$ là: