Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao

* Hướng dẫn giải

Đáp án C

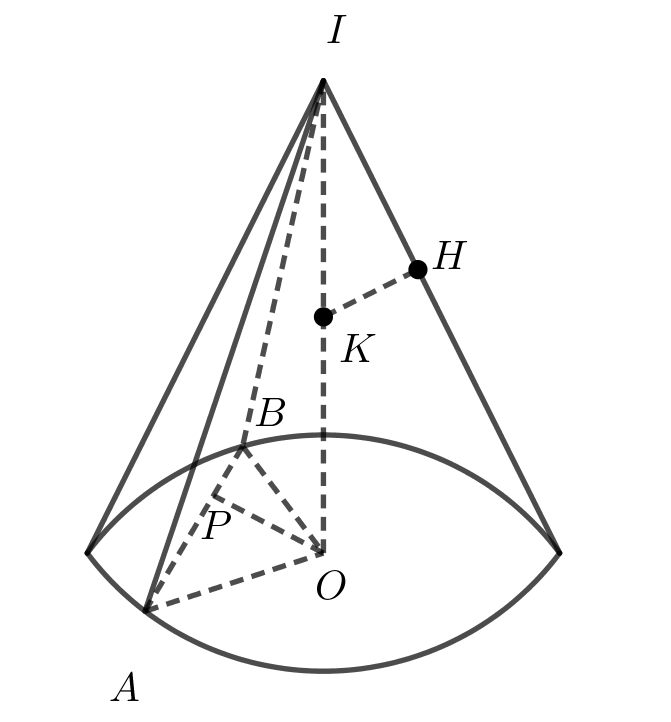
Gọi K là trung điểm của IO

$\Rightarrow KH=\sqrt{2}$

Do bán kính đáy (r) = chiều cao hình nón (h) 

nên tam giác thiết diện qua trục là tam giác vuông cân 

$$\begin{gathered} \Rightarrow \widehat{KIH}=45° \\ \Rightarrow ∆KIH vuông cân tại H \\ \Rightarrow IK=2 \Rightarrow IO = 4 = h = r \end{gathered}$$

Xét$∆OAB$, có: OB = OA = 4; AB = $\frac{1}{2}$

Nửa chu vi: $p=\frac{4+4+{\displaystyle \frac{1}{2}}}{2}=\frac{17}{4}$

Khi đó, diện tích $∆OAB$ là: $S_{∆OAB}=\sqrt{\frac{17}{4}\left(\frac{17}{4}-4\right)\left(\frac{17}{4}-4\right)\left(\frac{17}{4}-\frac{1}{2}\right)}=\frac{\sqrt{255}}{16}$

Thể tích hình chóp IOAB là: $V_{IOAB}=\frac{1}{3}.\frac{\sqrt{255}}{16}.4=\frac{\sqrt{255}}{12}$