Tính thể tích V của khối lăg trụ có đáy là một lục giác đều cạnh a và chiều cao của khối lăng trụ 4a.

* Hướng dẫn giải

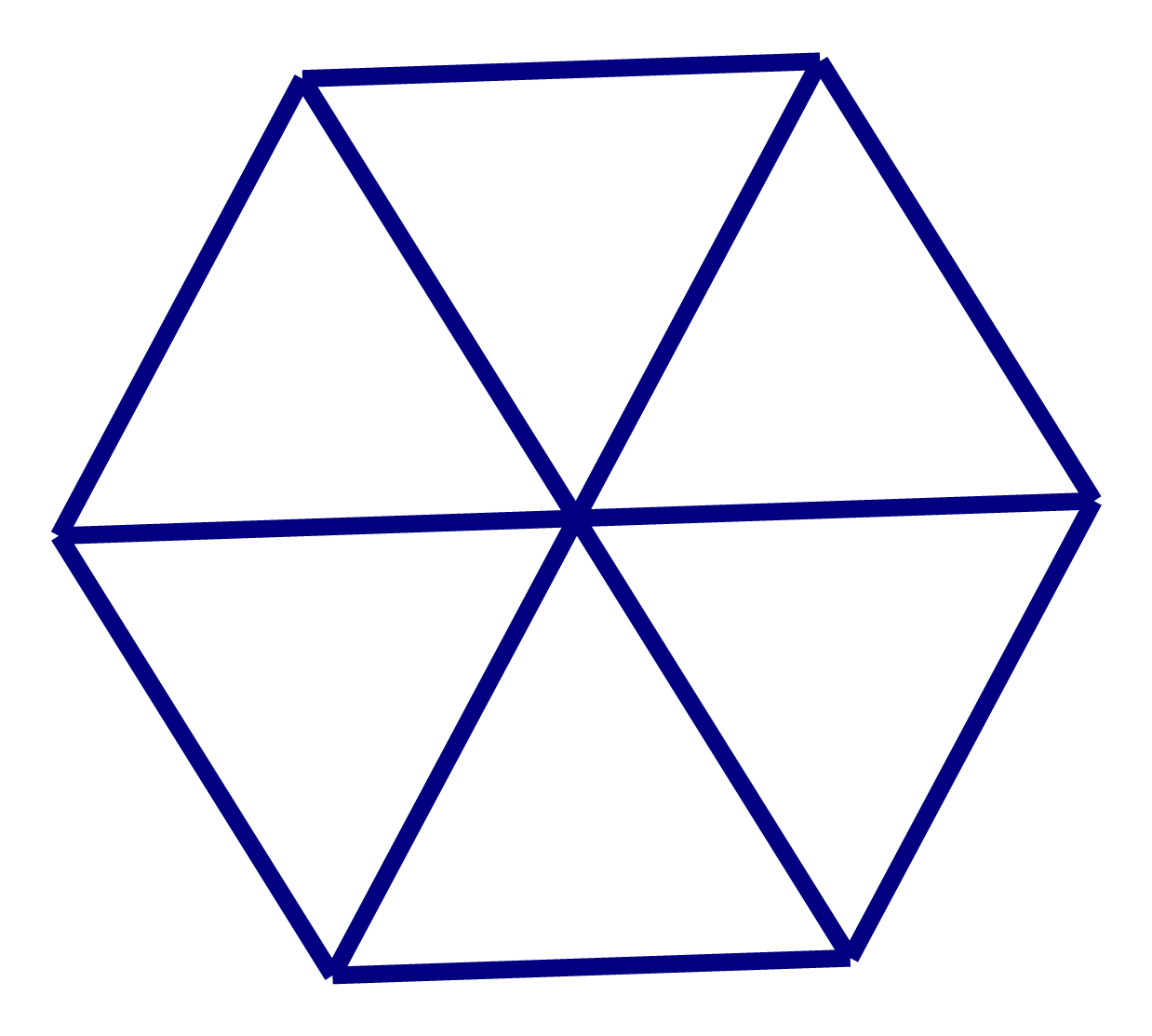
Hình lục giác đều cạnh a được tạo bởi 6 tam giác đều cạnh a.

Mỗi tam giác đều cạnh a có diện tích: \(S=\frac{{{a}^{2}}\sqrt{3}}{4}\).

Diện tích của hình lục giác đều là: \(S=6.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3}{2}{{a}^{2}}\sqrt{3}.\)

Thể tích của khối lăng trụ là: \(V=S.h=\frac{3}{2}{{a}^{2}}\sqrt{3}.4a=6\sqrt{3}{{a}^{3}}\).