Trong không gian Oxyz, cho hai vectơ a = (1; m; 2m - 1), b = (m + 1; m^2 + 1; 4m - 2)

* Hướng dẫn giải

Đáp án C

cos⁡($\overrightarrow{a}$; $\overrightarrow{b}$) đạt giá trị lớn nhất khi và chỉ khi góc giữa hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ là 0⁰, nghĩa là tồn tại một số dương k sao cho $\overrightarrow{a}$ = k $\overrightarrow{b}$

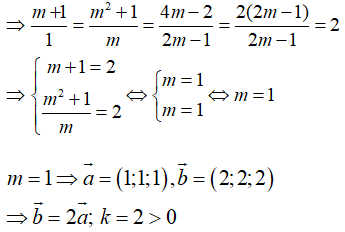
Vậy m = 1 thì thỏa mãn yêu cầu bài toán.