Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
100 câu trắc nghiệm Số phức nâng cao !!
Tính mô-đun của số phức z, biết z^3 + 12i...
Tính mô-đun của số phức z, biết z^3 + 12i = z ngang
Câu hỏi :
Tính mô-đun của số phức z, biết 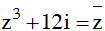 và z có phần thực dương.
và z có phần thực dương.
A. 2
B. 1
C.3
D.
* Đáp án
D
* Hướng dẫn giải
Chọn D.
Giả sử z = x + yi (x, y R); từ giả thiết :
Nên ( x + yi) 3+ 12i = x - yi
Hay x3 - 3xy2+ ( 3x2y - y3 +12) i = x - yi
Ta có hệ phương trình là x3 - 3xy2 = x (1) và 3x2y - y3 + 12 = - y ( 2)
Do x > 0 nên từ (1) x2 = 3y2+ 1. Thế vào (2) ta được:
3( 3y2 + 1) y - y3 + 12 = -y
Hay 2y3+ y + 3 = 0 (3)
Giải phương trình (3) ta được y = -1; x2 = 4. Do x > 0 nên x = 2.
Vậy z = 2 - i và
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
100 câu trắc nghiệm Số phức nâng cao !!
Số câu hỏi: 101
Copyright © 2021 HOCTAP247
