Bài tập 49 trang 32 SGK Toán 8 Tập 2
Bài tập 49 trang 32 SGK Toán 8 Tập 2
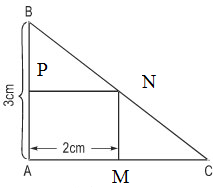
Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từu miếng bìa đó ra một hình chữ nhật có chiều dài 2cm như hình 5 thì hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
\(\frac{{MN}}{{AB}} = \frac{{MC}}{{AC}}hayMN = \frac{{AB.MC}}{{AC}} = \frac{{3.(x - 2)}}{x}\)
Diện tích hình chữ nhật MNPA là:
\(AM.MN = 2.\frac{{3.(x - 2)}}{x} = \frac{{6.(x - 2)}}{x}\)
Diện tích tam giác ABC là:
\(\frac{1}{2}.AB.AC = \frac{1}{2}.3.x = \frac{3}{2}x\)
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
\(\begin{array}{l}
\frac{3}{2}x = 2.\frac{{6.(x - 2)}}{x}\\
\Leftrightarrow \frac{{3{x^2}}}{{2x}} = \frac{{24.(x - 2)}}{{2x}}\\
\Leftrightarrow 3{x^2} = 24.(x - 2)\\
\Leftrightarrow {x^2} - 8x + 16 = 0\\
\Leftrightarrow {(x - 4)^2} = 0
\end{array}\)
\( \Leftrightarrow x = 4\) (thỏa mãn điều kiện)
Vậy độ dài đoạn thẳng AC là 4cm.
-- Mod Toán 8
Copyright © 2021 HOCTAP247