Bài tập 31 trang 23 SGK Toán 8 Tập 2
Bài tập 31 trang 23 SGK Toán 8 Tập 2
Giải các phương trình:
a) \(\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}\)
b) \(\frac{3}{(x-1)(x-2)}+\frac{2}{(x-3)(x-1)}=\frac{1}{(x-2)(x-3)}\)
c) \(1+\frac{1}{x+2}=\frac{12}{8+x^3}\)
d) \(\frac{13}{(x-3)(2x+7)}+\frac{1}{2x+7}=\frac{6}{(x-3)(x+3)}\)
Câu a:
\(\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}\)
Ta có: \(x^3-1=(x-1)(x^2+x+1)\)
\(=(x-1)[(x+\frac{1}{2})^2+\frac{3}{4}]\) cho nên x3 – 1 ≠ 0 khi x – 1 ≠ 0 ⇔ x ≠ 1
Vậy ĐKXĐ: x ≠ 1
Khử mẫu ta được:
\(x^2+x+1-3x^2=2x(x-1)\Leftrightarrow -2x^2+x+1=2x^2-2x\)
⇔4x2 − 3x − 1=0
⇔4x (x−1) + (x−1)=0
⇔(x−1)(4x+1)=0
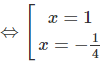
x = 1 không thỏa ĐKXĐ.
Vậy phương trình có nghiệm duy nhất x=−14x=−14
Câu b:
\(\frac{ 3}{(x-1)(x-2)}+\frac{2}{(x-3)(x-1)}=\frac{1}{(x-2)(x-3)}\)
ĐKXĐ: x ≠ 1, x ≠ 2, x ≠ 3
Khử mẫu ta được:
\(3(x-3)+2(x-2)=x-1\Leftrightarrow 3x-9+2x-4=x-1\)
⇔5x − 13= x − 1
⇔ 4x = 12
⇔ x = 3
x = 3 không thỏa mãn ĐKXĐ.
Vậy phương trình vô nghiệm.
Câu c:
\(1+\frac{1}{x+2}=\frac{12}{8+x^3}\)
Ta có: \(8+x^3=(x+2)(x^2-2x+4)\)
=(x + 2)[(x − 1)2+ 3]
Do đó: 8 + x2 ≠ 0 khi x + 2 ≠ 0 ⇔ x ≠ -2
Suy ra ĐKXĐ: x ≠ -2
Khử mẫu ta được:
\(x^3+8+x^2-2x+4=12\Leftrightarrow x^3+x^2-2x=0\)
⇔x(x2+x−2)=0
⇔x[x2 + 2x − x − 2]=0
⇔ x(x + 2)(x – 1) = 0
⇔ x(x -1) = 0
⇔x = 0 hay x = 1
x = 0, x = 1 thỏa ĐKXĐ của phương trình.
Vậy phương trình có tập nghiệm là S = {0;1}.
Câu d:
\(\frac{13}{(x-3)(2x+7)}+\frac{1}{2x+7}=\frac{6}{(x-3)(x+3)}\)
ĐKXĐ: \(x\neq 3,x\neq -3,x\neq -\frac{7}{2}\)
Khử mẫu ta được:
\(13(x+3)+(x-3)(x+3)=6(2x+7)\Leftrightarrow 13x+39+x^2-9=12x+42\)
⇔ x2 + x − 12=0
⇔ x2 + 4x − 3x − 12=0
⇔x(x+4) −3(x+4)=0
⇔(x−3)(x+4)=0
⇔ x =3 hoặc x = -4
x = 3 không thỏa ĐKXĐ.
Vậy phương trình có nghiệm duy nhất x = -4
-- Mod Toán 8
Copyright © 2021 HOCTAP247
