Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m
Câu hỏi :
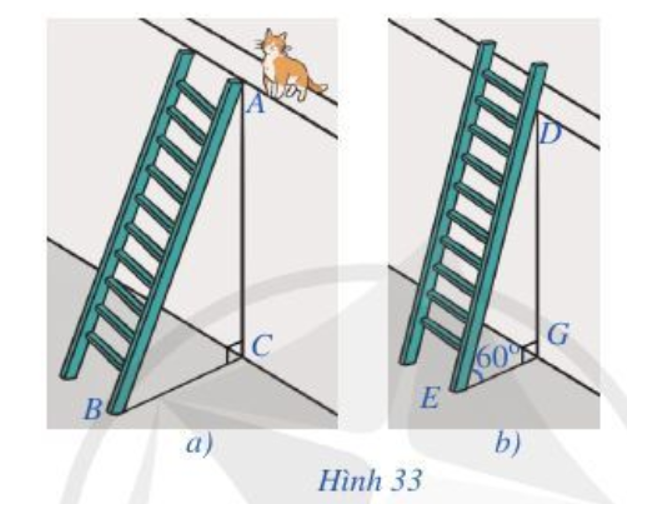
Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng và mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc 60° (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng và mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc 60° (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
* Đáp án
* Hướng dẫn giải
Gọi chiều cao của bức tường là x (mét) (x > 0).
Vì chiếc thang cao hơn tường 1 m nên chiều cao của chiếc thang là x + 1 (m).
Khi đó quan sát Hình 33a ta thấy, AC = x, AB = x + 1, tam giác ABC vuông tại C, áp dụng định lý Pythagore ta có: AB2 = AC2 + BC2
Suy ra: BC2 = AB2 – AC2 = (x + 1)2 – x2 = 2x + 1 (m).
Quan sát Hình 33b, ta thấy chiều cao bức tường không thay đổi nên DG = x (m).
Khi bác Nam dịch chuyển chân thang vào gần tường thêm 0,5 m thì GE = BC – 0,5.
Suy ra (m)
Lại có tam giác DGE vuông tại G nên ta có:
Mà , DG = x,
Do đó:
Suy ra:
(1)
Bình phương hai vế của (1) ta được:
Do x > 0 nên x ≈ 4,7 là giá trị thỏa mãn.
Vậy bức tường cao khoảng 4,7 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hai dạng phương trình quy về phương trình bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
