Quan sát đồ thị hàm số bậc hai y = ax2 + bx + c ở Hình 37a và Hình 37b rồi nêu

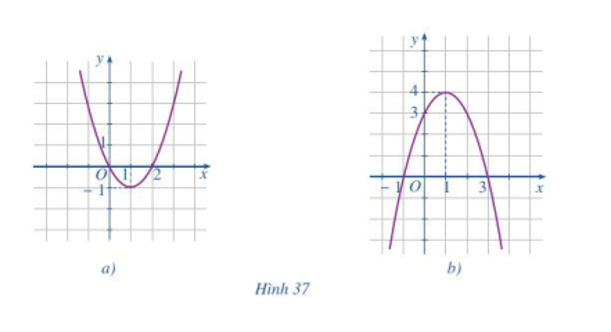
* Hình 37a: Quan sát đồ thị ta thấy:

a) Bề lõm của đồ thị hướng lên trên nên hệ số a > 0 hay hệ số a mang dấu “+”.

b) Tọa độ đỉnh I(1; – 1), trục đối xứng x = 1.

c) Do hệ số a > 0 nên hàm số đồng biến trên khoảng (1; + ∞).

d) Hàm số nghịch biến trên khoảng (– ∞; 1).

e) Phần parabol nằm phía trên trục hoành tương ứng với các khoảng (– ∞; 0) và (2; + ∞) nên hàm số y > 0 trên các khoảng giá trị của x là (– ∞; 0) ∪ (2; + ∞).

g) Phần parabol phía dưới trục hoành tương ứng với khoảng (0; 2) nên hàm số y < 0 trên (0; 2). Vậy khoảng giá trị của x mà y ≤ 0 là đoạn [0; 2].

* Hình 37b: Quan sát đồ thị ta thấy,

a) Bề lõm của đồ thị hướng xuống dưới nên a < 0 hay hệ số a mang dấu “–”.

b) Tọa độ đỉnh I(1; 4), trục đối xứng x = 1.

c) Do hệ số a < 0 nên hàm số đồng biến trên khoảng (– ∞; 1).

d) Hàm số nghịch biến trên khoảng (1; +∞).

e) Phần parabol nằm phía trên trục hoành tương ứng với khoảng (– 1; 3) nên khoảng giá trị của x là (– 1; 3) thì y > 0.

g) Phần parabol nằm phía dưới trục hoành tương ứng với các khoảng (– ∞; – 1) và (3; + ∞) nên khoảng giá trị của x để y ≤ 0 là (– ∞; – 1] ∪ [3; + ∞).