Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và
Câu hỏi :
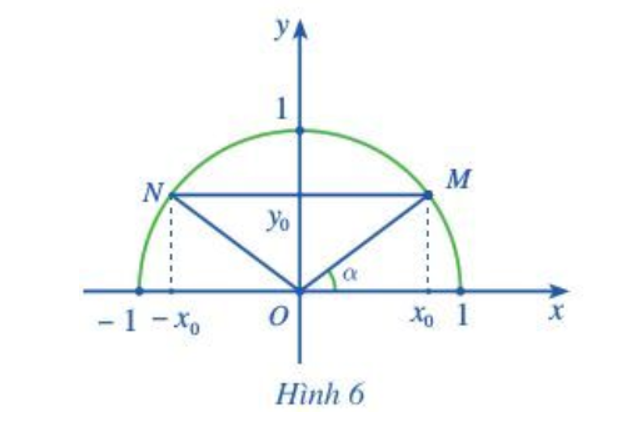
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và (Hình 6).
a) Chứng minh
b) Biểu diễn giá trị lượng giác của góc 180° – α theo giá trị lượng giác của góc α.
Trên nửa đường tròn đơn vị ta có dây cung MN song song với trục Ox và (Hình 6).
a) Chứng minh
b) Biểu diễn giá trị lượng giác của góc 180° – α theo giá trị lượng giác của góc α.
* Đáp án
* Hướng dẫn giải
a) Do MN // Ox nên (hai góc so le trong).
Tam giác OMN có OM = ON (bán kính) nên tam giác OMN cân tại O.
Suy ra .
Ta lại có:
Vậy
b) Do điểm M có tọa độ (x0; y0) thuộc nửa đường tròn đơn vị sao cho nên theo định nghĩa tỉ số lượng giác của góc có giá trị từ 0° đến 180° ta có:
sin α = y0; cos α = x0; ; (1).
Do điểm N có tọa độ (– x0; y0) thuộc nửa đường tròn đơn vị sao cho nên theo định nghĩa tỉ số lượng giác của góc có giá trị từ 0° đến 180° ta có:
sin(180° – α) = y0; cos(180° – α) = – x0;; (2).
Từ (1) và (2) ta có: sin(180° – α) = sin α;
cos(180° – α) = – cos α;
tan(180° – α) = – tan α;
cot(180° – α) = – cot α.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Giá trị lượng giá của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án !!
Copyright © 2021 HOCTAP247
