Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A
Câu hỏi :
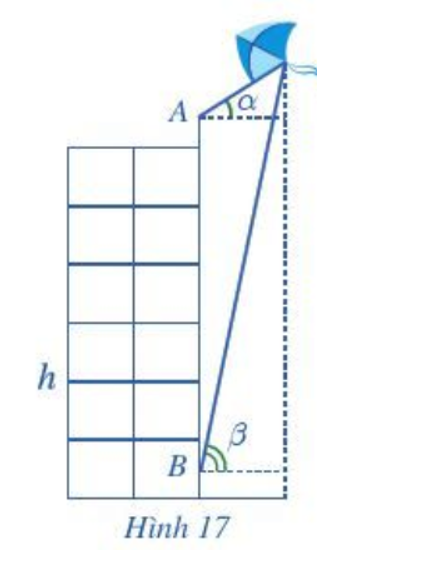
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là α = 35°; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là β = 75°; khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là α = 35°; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là β = 75°; khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?
* Đáp án
* Hướng dẫn giải
Ta đặt tên các điểm như trên hình vẽ dưới:
Ta có: AI là khoảng cách từ đỉnh của tòa nhà tới mắt bạn A nên AI = 1,5 m.
BE là khoảng cách từ mặt đất tới mắt của bạn B nên BE = 1,5 m.
Lại có: h = IB + BE ⇒ IB = h – BE = 20 – 1,5 = 18,5 (m).
Và AB = AI + IB = 1,5 + 18,5 = 20 (m).
Ta có: ;
Tam giác ABC có (định lí tổng ba góc trong tam giác)
Suy ra
Áp dụng định lí sin trong tam giác ABC ta có:
Do đó: .
Tam giác CBH vuông tại H nên
⇒ CH = BC . sin β = 25,5 . sin 75° ≈ 24,6.
Lại có HK = BE = 1,5 m.
Do đó CK = CH + HK = 24,6 + 1,5 = 26,1 (m).
Vậy chiếc diều bay cao 26,1 m so với mặt đất.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Giá trị lượng giá của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án !!
Copyright © 2021 HOCTAP247
