Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Giải tam giác có đáp án !!
Cho tam giác ABC có BC = a, CA =...
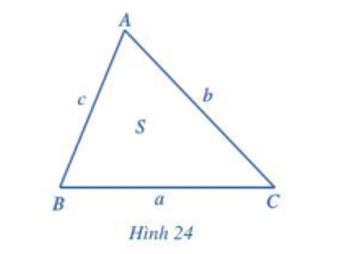
Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24)
Câu hỏi :
Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).
a) Từ định lí côsin, chứng tỏ rằng:
, ở đó .
b) Bằng cách sử dụng công thức , hãy chứng tỏ rằng:
.
Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).
a) Từ định lí côsin, chứng tỏ rằng:
, ở đó .
b) Bằng cách sử dụng công thức , hãy chứng tỏ rằng:
.
* Đáp án
* Hướng dẫn giải
a) Áp dụng định lí côsin trong tam giác ABC ta có:
BC2 = AB2 + AC2 – 2 . AB . AC . cos A
(1)
Ta lại có: sin2 A + cos2 A = 1
Do đó: sin2 A = 1 – cos2 A
Vì góc A là một góc của tam giác ABC nên 0° < < 180° nên sin A > 0.
Nên (2)
Từ (1) và (2) ta có:
Lại có
Khi đó:
Vậy .
b) Diện tích tam giác ABC là .
Mà
Nên .
Vậy .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Giải tam giác có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
