Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Giải tam giác có đáp án !!
Một người đi dọc bờ biển từ vị trí A...
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan
Câu hỏi :
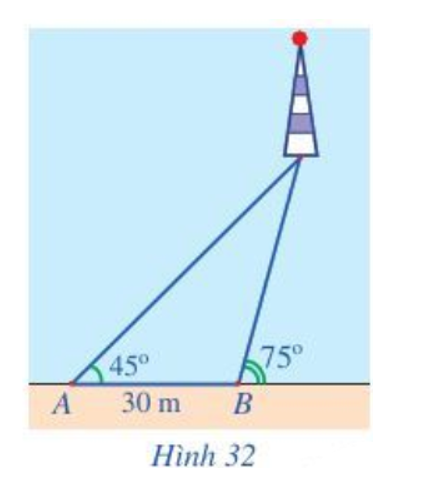
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45° và 75°. Biết khoảng cách giữa hai bị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45° và 75°. Biết khoảng cách giữa hai bị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
* Đáp án
* Hướng dẫn giải
Giả sử C là vị trí của ngọn hải đăng, kẻ CH vuông góc AB thì CH là khoảng cách giữa ngọn hải đăng và bờ.
Ta có: là góc ngoài tại đỉnh B của tam giác ABC.
Nên .
.
Áp dụng định lí sin trong tam giác ABC ta có:
.
Tam giác CBH vuông tại H nên
.
Vậy ngọn hải đăng cách bờ biển khoảng 41 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Giải tam giác có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
