Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập cuối chương IV có đáp án !!
Cho hình bình hành ABCD có AB = 4, AD...
Cho hình bình hành ABCD có AB = 4, AD = 6, góc BAD = 60 độ (Hình 73)
Câu hỏi :
Cho hình bình hành ABCD có AB = 4, AD = 6, (Hình 73).
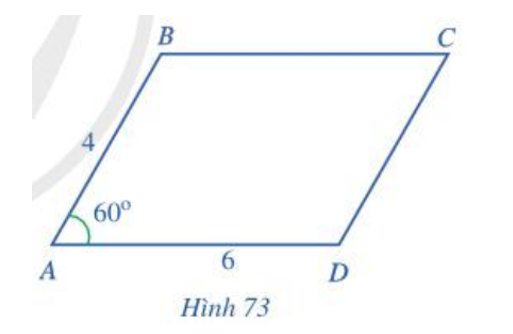
a) Biểu thị các vectơ theo .
b) Tính các tích vô hướng .
c) Tính độ dài các đường chéo BD, AC.
Cho hình bình hành ABCD có AB = 4, AD = 6, (Hình 73).
a) Biểu thị các vectơ theo .
b) Tính các tích vô hướng .
c) Tính độ dài các đường chéo BD, AC.
* Đáp án
* Hướng dẫn giải
a) Ta có: .
Do ABCD là hình bình hành nên .
b) Ta có:
= 4 . 6 . cos60° = 12.
Do đó:
Ta cũng có:
= AB2 + 12 = 42 + 12 = 28.
Do đó:
Lại có:
= AD2 – AB2 = 62 – 42 = 20.
Vậy
c) Áp dụng định lí côsin trong tam giác ABD có:
BD2 = AB2 + AD2 – 2 . AB . AD . cosA
= 42 + 62 – 2 . 4 . 6 . cos 60° = 28
Ta có:
Suy ra: AC2 = 42 + 2 . 12 + 62 = 76
.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập cuối chương IV có đáp án !!
Số câu hỏi: 38
Copyright © 2021 HOCTAP247
