Biểu diễn miền nghiệm của hệ bất phương trình (y - 2x) < = 2; y < = 4; x < = 5
Câu hỏi :
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ.
Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x;y) = - x – y với (x;y) thỏa mãn hệ trên.
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ.
Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x;y) = - x – y với (x;y) thỏa mãn hệ trên.
* Đáp án
* Hướng dẫn giải
Xác định miền nghiệm D1 của bất phương trình y – 2x ≤ 2 được xác định như sau:
- Vẽ đường thẳng d: -2x + y = 2.
- Ta lấy gốc tọa độ O(0;0) và tính -2.0 + 0 = 0 < 2.
Do đó miền nghiệm D1 là nửa mặt phẳng có bờ là đường thẳng d chứa gốc tọa độ.
Miền nghiệm D2 của bất phương trình y ≤ 4 là nửa mặt phẳng có bờ là đường thẳng y = 4 chứa gốc tọa độ.
Miền nghiệm D3 của bất phương trình x ≤ 5 là nửa mặt phẳng có bờ là đường thẳng x = 5 chứa gốc tọa độ.
Xác định miền nghiệm D4 của bất phương trình x + y ≥ - 1 được xác định như sau:
- Vẽ đường thẳng d’: x + y = -1.
- Ta lấy gốc tọa độ O(0;0) và tính 0 + 0 = 0 > -1.
Do đó miền nghiệm D4 là nửa mặt phẳng có bờ là đường thẳng d’ chứa gốc tọa độ.
Khi đó miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với tọa độ các điểm là: A(-1;0), B(1;4), C(5;4), D(5;-6).
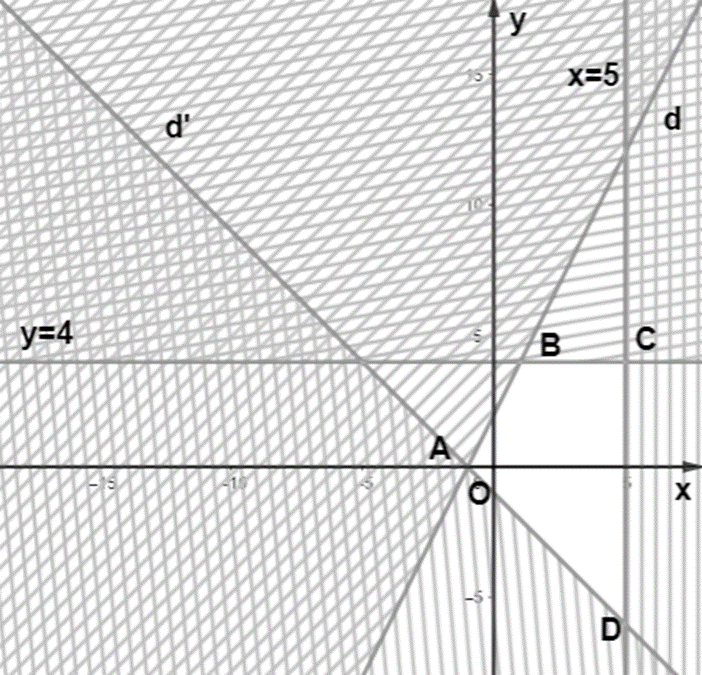
Tính giá trị biểu thức F(x;y) = - x – y tại các điểm A, B, C, D
F(-1;0) = -(-1) – 0 = 1;
F(1;4) = - 1 – 4 = -5;
F(5;4) = - 5 – 4 = -9;
F(5;-6) = - 5 – (-6) = 1.
Vậy giá trị lớn nhất của biểu thức F là 1 tại (x;y) = (-1;0) hoặc (x;y) = (5;-6) và giá trị nhỏ nhất của biểu thức F là -9 tại (x;y) = (5;4)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập ôn tập chương II có đáp án !!
Copyright © 2021 HOCTAP247
