Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập cuối chương III có đáp án !!
Cho tam giác ABC có trung tuyến AM. Chứng minh...
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
Câu hỏi :
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a)
b) MA2 + MB2 – AB2 = 2MA.MB.cos và MA2 + MC2 – AC2 = 2MA.MC.cos;
c) (công thức đường trung tuyến).
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a)
b) MA2 + MB2 – AB2 = 2MA.MB.cos và MA2 + MC2 – AC2 = 2MA.MC.cos;
c) (công thức đường trung tuyến).
* Đáp án
* Hướng dẫn giải
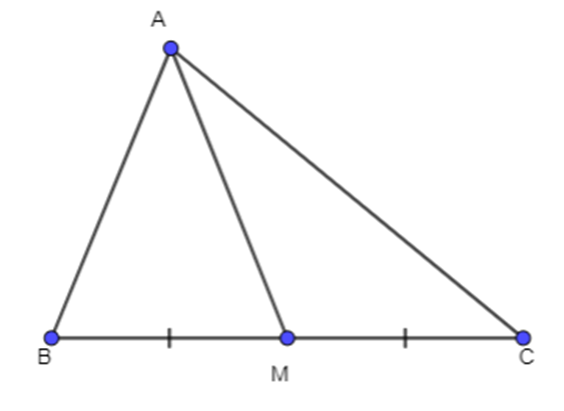
a)
Ta có:
b) Xét ΔAMB, ta có:
AB2 = MA2 + MB2 – 2MA.MB.cos
⇔ MA2 + MB2 – AB2 = 2MA.MB.cos (1)
Xét ΔAMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cos
⇔ MA2 + MC2 – AC2 = 2MA.MC.cos (2)
c) Cộng vế với vế của (1) với (2), ta được:
MA2 + MB2 – AB2 + MA2 + MC2 – AC2
= 2MA.MB.cos + 2MA.MC.cos
(Vì )
(vì )
(công thức đường trung tuyến).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập cuối chương III có đáp án !!
Số câu hỏi: 29
Copyright © 2021 HOCTAP247
