Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Các khái niệm mở đầu có đáp án !!
Cho hình vuông ABCD có hai đường chéo cắt nhau...
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập S gồm tất cả
Câu hỏi :
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập S gồm tất cả các vecto khác , có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập S gồm tất cả các vecto khác , có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
* Đáp án
* Hướng dẫn giải
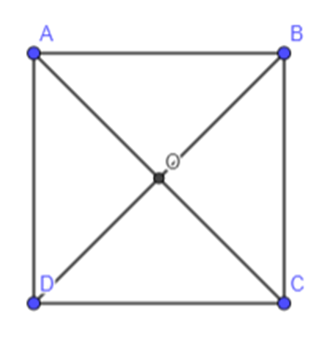
Các vecto khác , có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O} là:
Khi đó:
Hai vecto bằng nhau trong tập hợp S là:
Khi đó tập S được chia thành các nhóm là:
Nhóm 1:
Nhóm 2:
Nhóm 3:
Nhóm 4:
Nhóm 5:
Nhóm 6:
Nhóm 7:
Nhóm 8:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Các khái niệm mở đầu có đáp án !!
Số câu hỏi: 12
Copyright © 2021 HOCTAP247
