Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Tổng và hiệu của hai vectơ có đáp án !!
Cho tứ giác ABCD. Gọi M, N lần lượt là...
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O
Câu hỏi :
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng .
* Đáp án
* Hướng dẫn giải
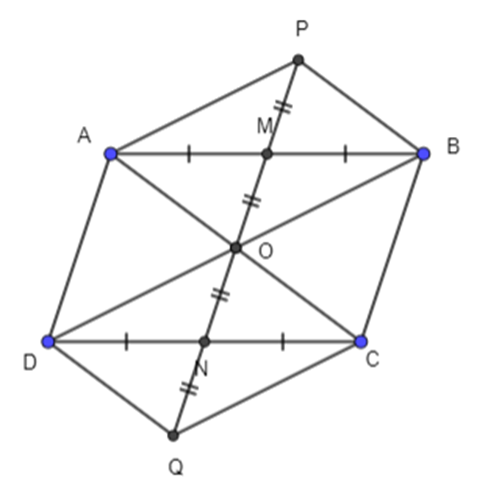
Gọi P và Q lần lượt là điểm đối xứng với O qua M và N.
Khi đó AOBP, DOCQ là các hình bình hành
(quy tắc hình bình hành)
(quy tắc hình bình hành)
Mà hai vecto và có cùng độ dài và ngược hướng nên chúng là hai vecto đối nhau, do đó
.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Tổng và hiệu của hai vectơ có đáp án !!
Số câu hỏi: 53
Copyright © 2021 HOCTAP247
