Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Tích của một vecto với một số có đáp án !!
Trong Hình 4.27, hãy biểu thị mỗi vecto vecto u,...
Trong Hình 4.27, hãy biểu thị mỗi vecto vecto u, vecto v theo hai vecto a, vecto b
Câu hỏi :
Trong Hình 4.27, hãy biểu thị mỗi vecto theo hai vecto , tức là tìm các số x, y, z, t để
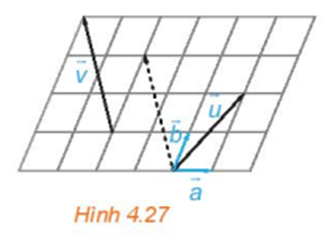

* Đáp án
* Hướng dẫn giải
Ta có hình vẽ sau:
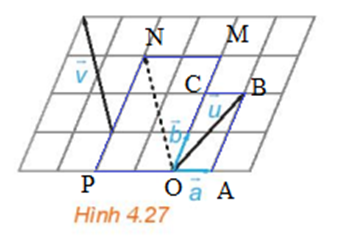
Xét hình bình hành OABC, có:
Khi đó, ta có:
(quy tắc hình bình hành)
Xét hình bình hành OMNP, có:
Khi đó, ta có:
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Tích của một vecto với một số có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
