Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80m, lúc đó máy bay đang bay với vận tốc
Câu hỏi :
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80m, lúc đó máy bay đang bay với vận tốc 50m/s. Để thùng hàng hỗ trợ rơi trúng vị trí được chọn, máy bay cần thả hàng ở vị trí nào? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau:
Trong đó, v0 là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80m, lúc đó máy bay đang bay với vận tốc 50m/s. Để thùng hàng hỗ trợ rơi trúng vị trí được chọn, máy bay cần thả hàng ở vị trí nào? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau:
Trong đó, v0 là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.

* Đáp án
* Hướng dẫn giải
Gọi A là vị trí bắt đầu thả hàng, C là vị trí được chọn để nhận thùng hàng hỗ trợ.
Ta có O là hình chiếu của A trên mặt đất nên ta có hình vẽ sau:
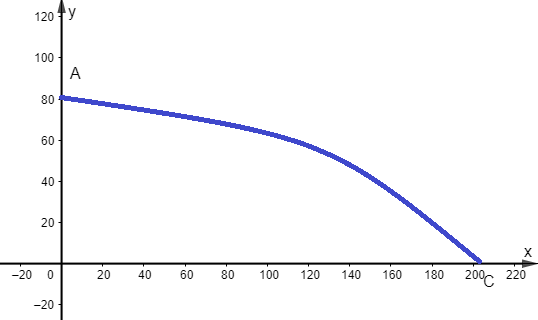
Tọa độ điểm C là nghiệm của hệ phương trình:
với h = 80m, g = 9,8m/s2, v0 = 50m/s.
Do C ở mặt đất nên tung độ của C là yC = 0. Khi đó ta có hệ phương trình:
Vậy vị trí được chọn để nhận thùng hàng hỗ trợ có tọa độ là (202,03; 0).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập cuối chương III có đáp án !!
Copyright © 2021 HOCTAP247
