Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có: a) cos2α + sin2α = 1
Câu hỏi :
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có:
a) cos2α + sin2α = 1;
b) tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).
c) 1 + tan2α = (α ≠ 90°);
d) 1 + cot2 α = (0° < α < 180°).
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có:
a) cos2α + sin2α = 1;
b) tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).
c) 1 + tan2α = (α ≠ 90°);
d) 1 + cot2 α = (0° < α < 180°).
* Đáp án
* Hướng dẫn giải
a) Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho .
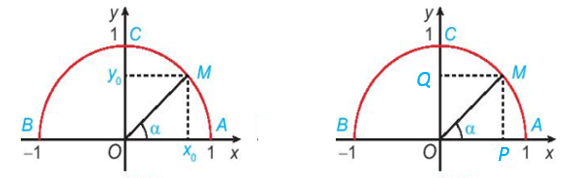
Gọi P, Q tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Áp dụng định lý Pythagore cho tam giác OPM vuông tại P có cạnh huyền OM = 1.
Ta có: OP2 + MP2 = OM2
Mà OP = |x0| ; MP = OQ = y0 và OM = 1
Suy ra : |x0|2 + y02 = 1 tức là x02 + y02 = 1 (vì |x0|2 = x02)
Mặt khác, theo định nghĩa giá trị lượng giác của một góc ta có:
sinα = y0
cosα = x0
Suy ra cos2 α + sin 2 α = x02 + y02 = 1
Vậy sin 2 α + cos2 α = 1.
b) Với mỗi góc α (0° < α < 180°, α ≠ 90°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho .
Khi đó tanα = ; cotα = ;
Suy ra tanα . cotα = . = 1.
Vậy tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).
c) Với α ≠ 90° ; tanα = và x02 + y02 = sin 2α + cos2α = 1 ; cosα = x0 ⇒ cos2α = x02.
Ta có: 1 + tan2α =
.
Vậy 1 + tan2α = (α ≠ 90°).
d) Với 0° < α < 180° ta có cotα = và sinα = y0 ⇒ sin2 α = y02.
Ta có : 1 + cot2α =
.
Vậy 1 + cot2 α = (0o < α < 180°).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Giá trị lượng giác của một góc từ 0° đến 180° có đáp án !!
Copyright © 2021 HOCTAP247
