a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và . Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
Câu hỏi :
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và . Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
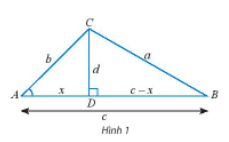
Hãy thay ? bằng chữ cái thích hợp để chứng minh công thức a2 = b2 + c2 – 2bccosA theo gợi ý sau:
Xét tam giác vuông BCD, ta có: a2 = d2 + (c – x)2 = d2 + x2 + c2 – 2xc. (1)
Xét tam giác vuông ACD, ta có: b2 = d2 + x2 ⇒ d2 = b2 – x2 (2)
cosA = ⇒ ? = bcosA. (3)
Thay (2) và (3) vào (1), ta có: a2 = b2 + c2 – 2bccosA.
Lưu ý : Nếu thì ta vẽ đường cao BD và chứng minh tương tự.
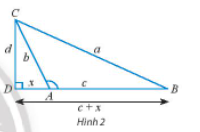
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
a2 = b2 + c2 – 2bccosA.
Lưu ý: Vì A tù nên cosA = .
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ công thức a2 = b2 + c2 – 2bccosA có thể viết là a2 = b2 + c2.
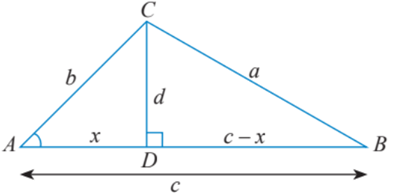
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và . Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.

Hãy thay ? bằng chữ cái thích hợp để chứng minh công thức a2 = b2 + c2 – 2bccosA theo gợi ý sau:
Xét tam giác vuông BCD, ta có: a2 = d2 + (c – x)2 = d2 + x2 + c2 – 2xc. (1)
Xét tam giác vuông ACD, ta có: b2 = d2 + x2 ⇒ d2 = b2 – x2 (2)
cosA = ⇒ ? = bcosA. (3)
Thay (2) và (3) vào (1), ta có: a2 = b2 + c2 – 2bccosA.
Lưu ý : Nếu thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
a2 = b2 + c2 – 2bccosA.
Lưu ý: Vì A tù nên cosA = .

c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ công thức a2 = b2 + c2 – 2bccosA có thể viết là a2 = b2 + c2.
* Đáp án
* Hướng dẫn giải
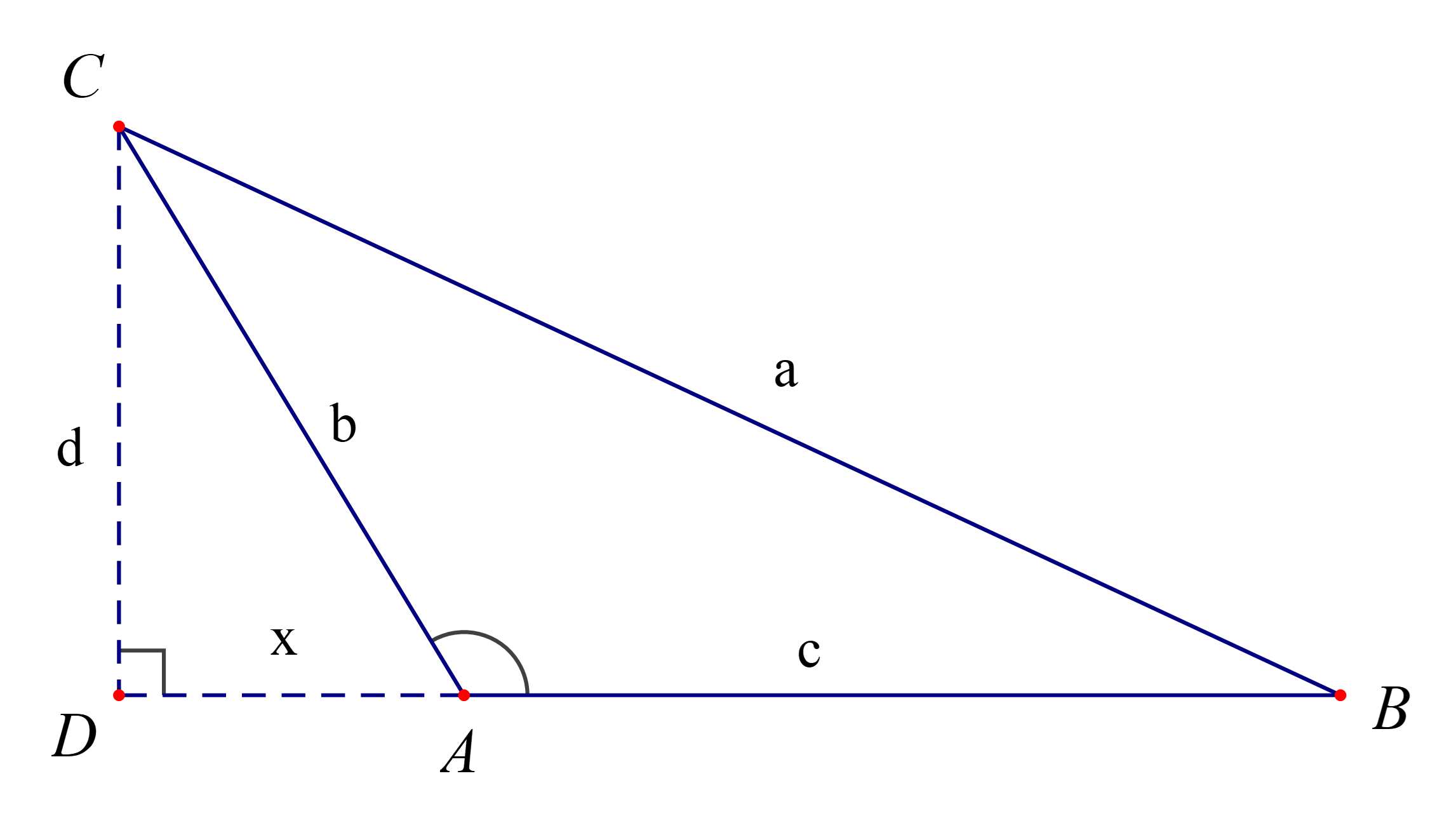
a)
Xét tam giác vuông ACD, ta có: cosA = ⇒ x = bcosA.
Vậy lời giải đúng:
Xét tam giác vuông BCD, ta có: a2 = d2 + (c – x)2 = d2 + x2 + c2 – 2xc. (1)
Xét tam giác vuông ACD, ta có: b2 = d2 + x2 ⇒ d2 = b2 – x2 (2)
cosA = ⇒ x = bcosA. (3)
Thay (2) và (3) vào (1), ta có : a2 = b2 + c2 – 2bccosA.
b) Với tam giác ABC có góc A tù :
Xét tam giác vuông BCD, ta có: a2 = d2 + (x + c)2 = d2 + x2 + c2 + 2xc. (4)
Xét tam giác vuông ACD, ta có: b2 = d2 + x2 ⇒ d2 = b2 – x2 (5)
cos = .
Do .
Suy ra: cos = cos = – cos =
⇒ cos =
⇒ x = –bcos , tức là x = – bcosA (6)
Thay (5) và (6) vào (4), ta được : a2 = b2 + c2 _ 2bccosA.
Vậy với tam giác ABC có góc A tù ta cũng có : a2 = b2 + c2 – 2bccosA.
c) Với tam giác ABC vuông tại A thì cosA = cos90° = 0.
Suy ra a2 = b2 + c2 – 2bccosA = b2 + c2 – 2bc.0 = b2 + c2.
Vậy a2 = b2 + c2.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Định lí côsin và định lí sin có đáp án !!
Copyright © 2021 HOCTAP247
