Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Định lí côsin và định lí sin có đáp án !!
Cho tam giác ABC có AB = 6, AC =...
Cho tam giác ABC có AB = 6, AC = 8 và . a) Tính diện tích tam giác ABC. b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC
Câu hỏi :
Cho tam giác ABC có AB = 6, AC = 8 và .
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.
Cho tam giác ABC có AB = 6, AC = 8 và .
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.
* Đáp án
* Hướng dẫn giải
a) Áp dụng công thức tính diện tích tam giác ta có:
Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).
b) Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA = 62 + 82 – 2.6.8.cos60° = 52
⇒ BC = ≈ 7,2.
Mặt khác diện tích tam giác ABC:
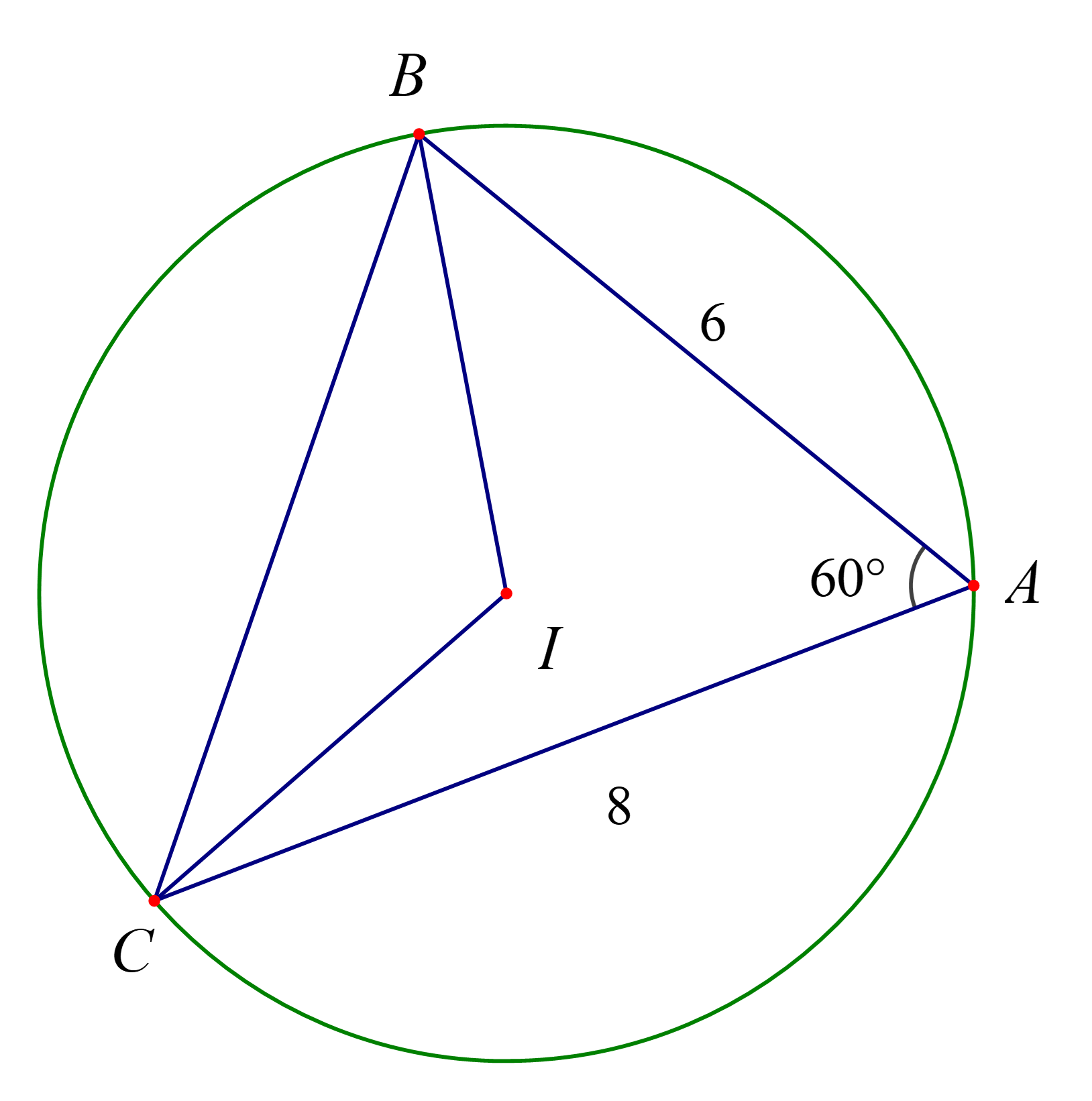
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.
Nửa chu vi của tam giác IBC:
Áp dụng công thức Heron ta tính được diện tích tam giác IBC:
Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Định lí côsin và định lí sin có đáp án !!
Số câu hỏi: 21
Copyright © 2021 HOCTAP247
