Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao. a) Chứng minh

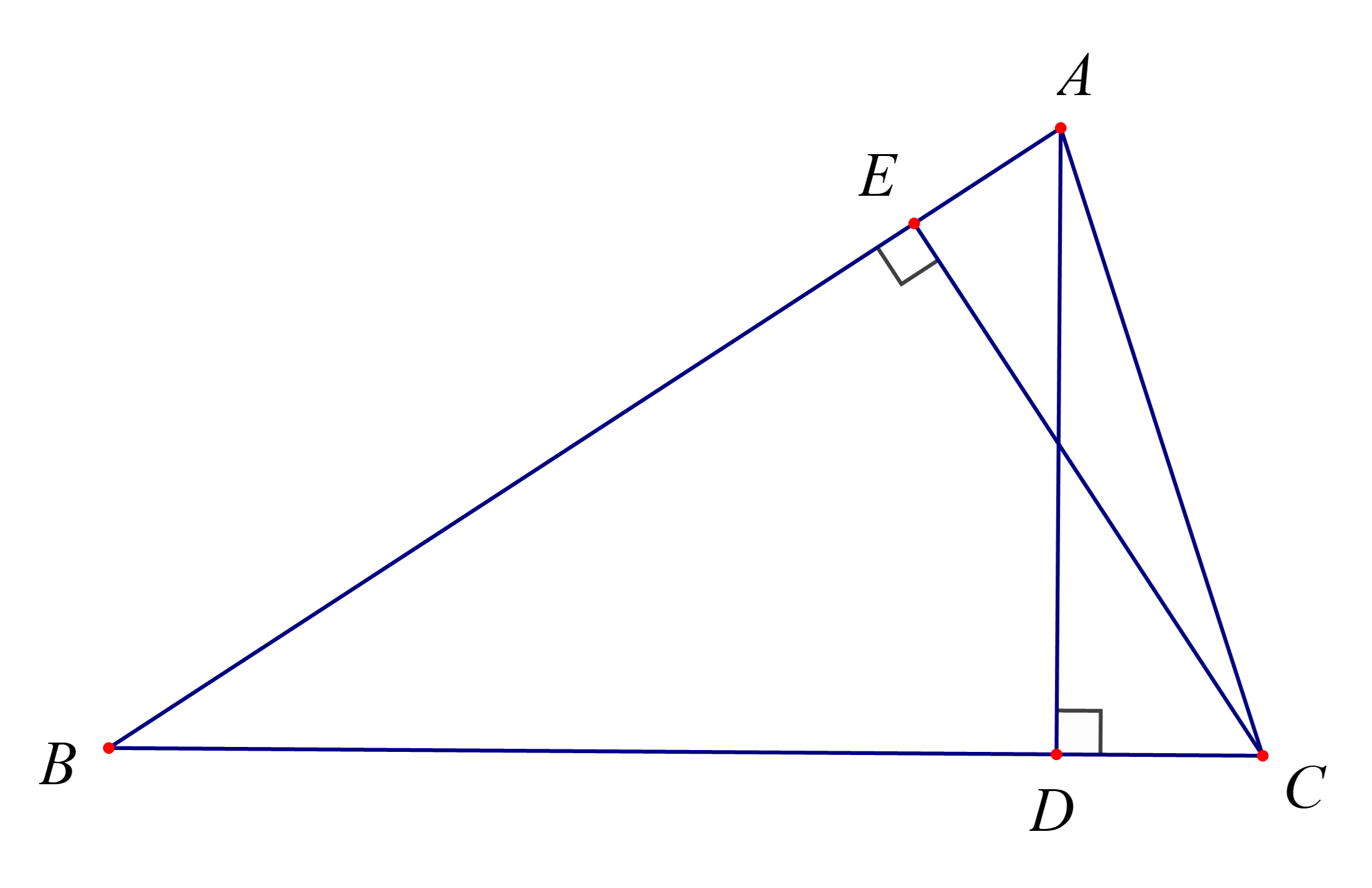
a) Áp dụng công thức tính diện tích tam giác cho hai tam giác BDE và tam giác ABC ta có:

$S_{BDE}=\frac{1}{2}.BD.BE.\sin B$

$S_{ABC}=\frac{1}{2}.BA.BC.\sin B$

Suy ra $\frac{S_{BDE}}{S_{BAC}}=\frac{\frac{1}{2}BD.BE.\sin B}{\frac{1}{2}BA.BC.\sin B}=\frac{BD.BE}{BA.BC}$

Vậy $\frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}$

b) Từ S_ABC = 9S_BDE ⇒ $\frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}=\frac{1}{9}$

Tam giác BEC vuông tại E có: cosB = $\frac{BE}{BC}$ .

Tam giác ADB vuông tại D có: cosB = $\frac{BD}{AB}$ .

Suy ra cos²B = $\frac{BE}{BC}$. $\frac{BD}{AB}$ = $\frac{BD.BE}{BA.BC}=\frac{1}{9}$

$\Rightarrow \cos B=\pm \frac{1}{3}$

Mặt khác, vì góc B nhọn nên sinB > 0, cosB > 0, do đó: cosB = $\frac{1}{3}$.

Mà sin²B + cos²B = 1, suy ra sinB = 

$\sqrt{1-{\cos }^{2}B}=\sqrt{1-{\left(\frac{1}{3}\right)}^2}=\frac{2\sqrt{2}}{3}$

Xét hai tam giác BDE và tam giác BAC có:

$\frac{BE}{BC}$= $\frac{BD}{AB}$=  $\frac{1}{3}$(cùng bằng cosB)

Góc B chung

Suy ra hai tam giác BDE và tam giác BAC đồng dạng theo hệ số tỉ lệ k =$\frac{1}{3}$ .

⇒ $\frac{DE}{AC}=\frac{1}{3}\Rightarrow AC=3DE=3.2\sqrt{2}=6\sqrt{2}$

Áp dụng định lí sin cho hai tam giác BAC và tam giác BDE ta có:

$\frac{AC}{\sin B}=2R$; $\frac{DE}{\sin B}=2R\text{'}\Rightarrow R\text{'}=\frac{DE}{2\sin B}=\frac{2\sqrt{2}}{2.\frac{2\sqrt{2}}{3}}=\frac{3}{2}$(R’ là bán kính đường tròn ngoại tiếp tam giác BDE).

⇒ R = 3R' = $3.\frac{3}{2}=\frac{9}{2}$

Vậy cosB = $\frac{1}{3}$ ; R = $\frac{9}{2}$ .