Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích của tứ giác ABCD.

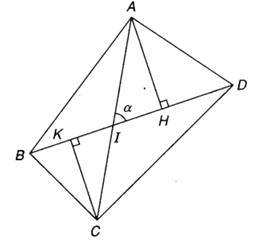
a) Ta có S_ABCD = S_ABD + S_CBD.

Vẽ AH và CK vuông góc với BD tại H và K.

Gọi I là giao điểm của hai đường chéo AC và BD.

Ta có : AH = AI.sinα ; CK = CI.sinα.

$S_{ABCD}=\frac{1}{2}AH.BD+\frac{1}{2}CK.BD=\frac{1}{2}BD.(AH+CK)=\frac{1}{2}BD.(AI+IC)\sin \alpha =\frac{1}{2}BD.AC\sin \alpha$

⇒ $S_{ABCD}=\frac{1}{2}x.y\sin \alpha$

b) Nếu AC ⊥ BD thì sinα = sin90° = 1, khi đó $S_{ABCD}=\frac{1}{2}x.y$

Như vậy nếu tứ giác lồi có hai đường chéo vuông góc với nhau thì diện tích của tứ giác đó bằng một nửa tích độ dài của hai đường chéo.