Tính chất của các số C k n a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
Câu hỏi :
Tính chất của các số
a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = ...
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = ...
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn, và , và . Từ đó hãy dự đoán hệ thức giữa và (0 ≤ k ≤ n).
b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
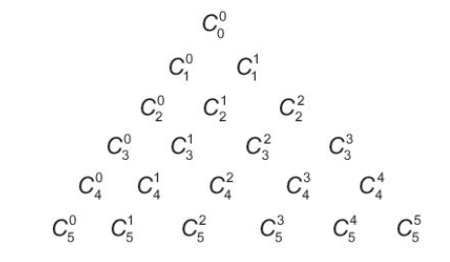
(a + b)1
(a + b)2
(a + b)3
(a + b)4
(a + b)5
Từ tính chất của tam giác Pascal, hãy so sánh và và Từ đó hãy dự đoán hệ thức giữa và
Tính chất của các số
a) Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu:
(a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = ...
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = ...
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn, và , và . Từ đó hãy dự đoán hệ thức giữa và (0 ≤ k ≤ n).
b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
(a + b)1
(a + b)2
(a + b)3
(a + b)4
(a + b)5
Từ tính chất của tam giác Pascal, hãy so sánh và và Từ đó hãy dự đoán hệ thức giữa và
* Đáp án
* Hướng dẫn giải
a) (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = a4 + a3b + a2b2 + ab3 + b4.
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
= a5 + a4b + a3b2 + a2b3 + ab4 + b5.
Ta thấy = , = ,...
Dự đoán: = .
b) Ta thấy = =
Dự đoán: =
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Nhị thức newton có đáp án !!
Copyright © 2021 HOCTAP247
