Bằng cách tô màu trên lưới ô vuông như hình dưới đây, một học sinh phát hiện ra công thức sau: 1 + 3 + 5 + 7 +... + (2n – 1) = n2. (1) a) Hãy chỉ ra công thức (1) đúng với n = 1, 2...
Câu hỏi :
Bằng cách tô màu trên lưới ô vuông như hình dưới đây,
một học sinh phát hiện ra công thức sau:
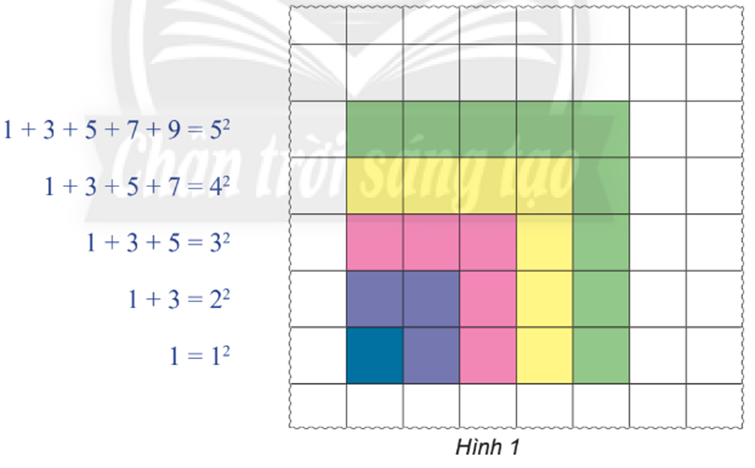
1 + 3 + 5 + 7 +... + (2n – 1) = n2. (1)
a) Hãy chỉ ra công thức (1) đúng với n = 1, 2, 3, 4, 5.
b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên n ≥ 1. Khẳng định như vậy đã thuyết phục chưa? Tại sao?
Bằng cách tô màu trên lưới ô vuông như hình dưới đây,
một học sinh phát hiện ra công thức sau:

1 + 3 + 5 + 7 +... + (2n – 1) = n2. (1)
a) Hãy chỉ ra công thức (1) đúng với n = 1, 2, 3, 4, 5.
b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên n ≥ 1. Khẳng định như vậy đã thuyết phục chưa? Tại sao?
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
a) Với n = 1, ta có 2.1 – 1 = 1 = 12, do đó công thức (1) đúng với n = 1.
Với n = 2, ta có 1 + (2.2 – 1) = 4 = 22, do đó công thức (1) đúng với n = 2.
Với n = 3, ta có 1 + 3 + (2.3 – 1) = 9 = 32, do đó công thức (1) đúng với n = 3.
Với n = 4, ta có 1 + 3 + 5 + (2.4 – 1) = 16 = 42, do đó công thức (1) đúng với n = 4.
Với n = 5, ta có 1 + 3 + 5 + 7 + (2.5 – 1) = 25 = 52, do đó công thức (1) đúng với n = 5.
b) Mỗi lần tô thêm một hàng và cột những ô vuông, bạn học sinh đã kiểm nghiệm công thức (1) thêm một trường hợp của n. Tuy nhiên, bới tập hợp ℕ* là vô hạn nên cách làm đó không thể chứng tỏ công thức (1) đúng với mọi n ℕ*.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Phương pháp quy nạp toán học có đáp án !!
Copyright © 2021 HOCTAP247
