Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trình chính tắc
Câu hỏi :
Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trình chính tắc là trong đó a > b > 0. Cho điểm M(x; y) nằm trên (E) (Hình 3).
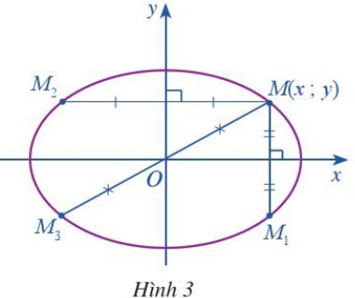
a) Gọi M1 là điểm đối xứng của M qua trục Ox. Tìm toạ độ của điểm M1. Điểm M1 có nằm trên (E) hay không? Tại sao?
b) Gọi M2 là điểm đối xứng của M qua trục Oy. Tìm toạ độ của điểm M2. Điểm M2 có nằm trên (E) hay không? Tại sao?
c) Gọi M3 là điểm đối xứng của M qua gốc O. Tìm toạ độ của điểm M3. Điểm M3 có nằm trên (E) hay không? Tại sao?
Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trình chính tắc là trong đó a > b > 0. Cho điểm M(x; y) nằm trên (E) (Hình 3).

a) Gọi M1 là điểm đối xứng của M qua trục Ox. Tìm toạ độ của điểm M1. Điểm M1 có nằm trên (E) hay không? Tại sao?
b) Gọi M2 là điểm đối xứng của M qua trục Oy. Tìm toạ độ của điểm M2. Điểm M2 có nằm trên (E) hay không? Tại sao?
c) Gọi M3 là điểm đối xứng của M qua gốc O. Tìm toạ độ của điểm M3. Điểm M3 có nằm trên (E) hay không? Tại sao?
* Đáp án
* Hướng dẫn giải
Theo đề bài, M(x; y) nằm trên (E) nên ta có:
a) M1 là điểm đối xứng của M qua trục Ox, suy ra M1 có toạ độ là (x; –y).
Ta có Do đó M1 cũng thuộc (E).
b) M2 là điểm đối xứng của M qua trục Oy, suy ra M2 có toạ độ là (–x; y).
Ta có Do đó M2 cũng thuộc (E).
c) M3 là điểm đối xứng của M qua gốc O, suy ra M3 có toạ độ là (–x; –y).
Ta có Do đó M3 cũng thuộc (E).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Elip có đáp án !!
Copyright © 2021 HOCTAP247
