Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Elip có đáp án !!
Cho elip (E) có phương trình chính tắc là x^2/a^2...
Cho elip (E) có phương trình chính tắc là x^2/a^2 + y^2/b^2 = 1 (a > b > 0).
Câu hỏi :
Cho elip (E) có phương trình chính tắc là (a > b > 0). Xét đường thẳng Δ1: x =
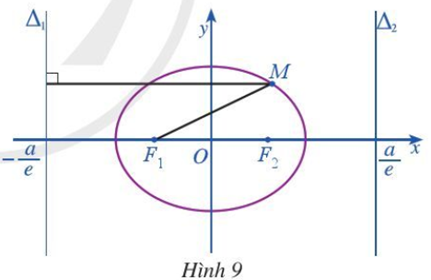
Với mỗi điểm M(x; y) (E) (Hình 9), tính:
a) Khoảng cách d(M, Δ1) từ điểm M(x; y) đến đường thẳng Δ1.
b) Tỉ số .
Cho elip (E) có phương trình chính tắc là (a > b > 0). Xét đường thẳng Δ1: x =

Với mỗi điểm M(x; y) (E) (Hình 9), tính:
a) Khoảng cách d(M, Δ1) từ điểm M(x; y) đến đường thẳng Δ1.
b) Tỉ số .
* Đáp án
* Hướng dẫn giải
a) Viết lại phương trình đường thẳng Δ1 ở dạng: Với mỗi điểm M(x; y) thuộc (E), ta có:
b) Do MF1 = a + ex > 0 nên MF1 = |a + ex|, suy ra . Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Elip có đáp án !!
Số câu hỏi: 50
Copyright © 2021 HOCTAP247
