Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Elip có đáp án !!
Cho elip (E) có phương trình chính tắc là x^2/a^2...
Cho elip (E) có phương trình chính tắc là x^2/a^2 + y^2/b^2 = 1 (a > b > 0).
Câu hỏi :
Cho elip (E) có phương trình chính tắc là (a > b > 0). Xét đường tròn (C) tâm O bán kính a có phương trình là x2 + y2 = a2.
Xét điểm M(x; y)(E) và điểm M1(x; y1)(C) sao cho y và y1 luôn cùng dấu (khi M khác với hai đỉnh A1, A2 của (E)) (Hình 10).
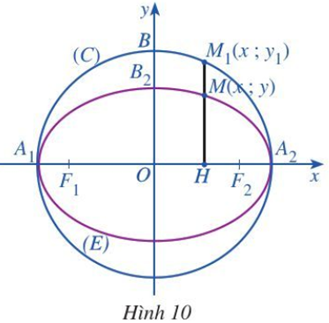
a) Từ phương trình chính tắc của elip (E), hãy tính y2 theo x2.
Từ phương trình của đường tròn (C), hãy tính y12 theo x2.
b) Tính tỉ số theo a và b.
Cho elip (E) có phương trình chính tắc là (a > b > 0). Xét đường tròn (C) tâm O bán kính a có phương trình là x2 + y2 = a2.
Xét điểm M(x; y)(E) và điểm M1(x; y1)(C) sao cho y và y1 luôn cùng dấu (khi M khác với hai đỉnh A1, A2 của (E)) (Hình 10).

a) Từ phương trình chính tắc của elip (E), hãy tính y2 theo x2.
Từ phương trình của đường tròn (C), hãy tính y12 theo x2.
b) Tính tỉ số theo a và b.
* Đáp án
* Hướng dẫn giải
a) Ta có:
b) Từ a) ta suy ra Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Elip có đáp án !!
Số câu hỏi: 50
Copyright © 2021 HOCTAP247
