Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Nhị thức newton có đáp án !!
Từ các công thức khai triển: (a + b)^0 =...
Từ các công thức khai triển: (a + b)^0 = 1; (a + b)^1 = a + b; (a + b)^2 = a^2 + 2ab + b^2
Câu hỏi :
Từ các công thức khai triển:
= 1;
= a + b;
;
;
các hệ số được viết thành bảng số như Hình 2 sau đây. Nếu sử dụng kí hiệu tổ hợp thì nhận được bảng như Hình 3.
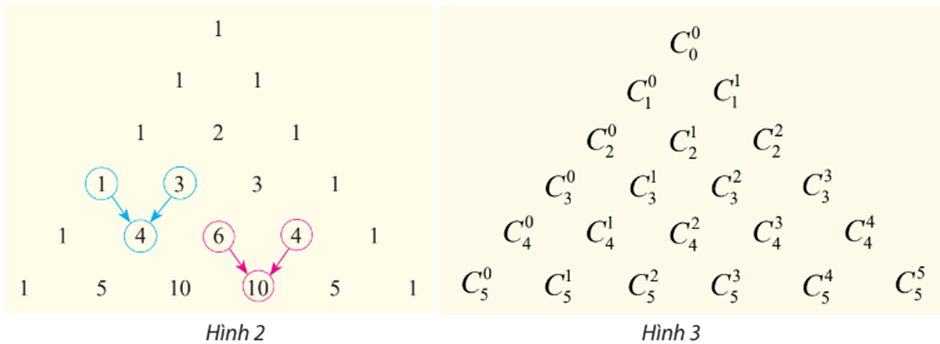
Từ các đẳng thức như
có thể dự đoán rằng, với mỗi ,
Hãy chứng minh các công thức trên.
Gợi ý: Sử dụng công thức
Từ các công thức khai triển:
= 1;
= a + b;
;
;
các hệ số được viết thành bảng số như Hình 2 sau đây. Nếu sử dụng kí hiệu tổ hợp thì nhận được bảng như Hình 3.

Từ các đẳng thức như
có thể dự đoán rằng, với mỗi ,
Hãy chứng minh các công thức trên.
Gợi ý: Sử dụng công thức
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
+) Có
Vậy
+)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Nhị thức newton có đáp án !!
Số câu hỏi: 50
Copyright © 2021 HOCTAP247
