Cho điểm M(x; y) nằm trên hypebol (H): x^2/a^2 - y^2/b^2 = 1 . a) Chứng minh rằng F1M2 – F2M2 = 4cx. b) Giả sử điểm M(x; y) thuộc nhánh đi qua A1(–a; 0) (Hình 5a). Sử dụng kết quả...
Câu hỏi :
Cho điểm M(x; y) nằm trên hypebol .
a) Chứng minh rằng F1M2 – F2M2 = 4cx.
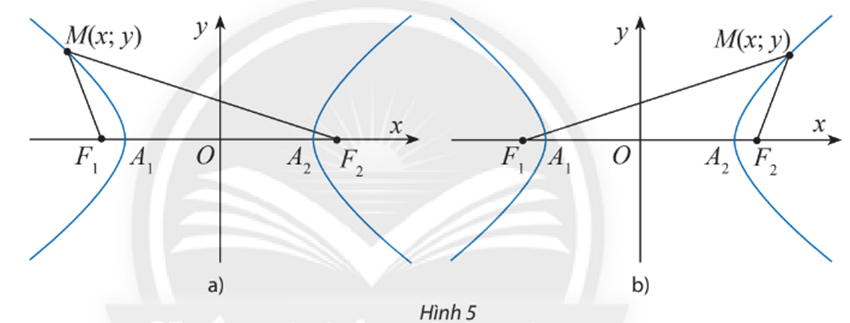
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A1(–a; 0) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF2 – MF1 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A2(a; 0) (Hình 5 b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF1 – MF2 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
Cho điểm M(x; y) nằm trên hypebol .
a) Chứng minh rằng F1M2 – F2M2 = 4cx.
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A1(–a; 0) (Hình 5a). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF2 – MF1 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;
b) Giả sử điểm M(x; y) thuộc nhánh đi qua A2(a; 0) (Hình 5 b). Sử dụng kết quả đã chứng minh được ở câu a) kết hợp với tính chất MF1 – MF2 = 2a đã biết để chứng minh . Từ đó, chứng minh các công thức: ;

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
a) F1M2 = + = + = ;
F2M2 = +=
F1M2 – F2M2 = () – () = 4cx.
b) Ta có: MF12 – MF22 = 4cx => (MF1 + MF2)(MF1 – MF2) = 4cx => (MF1 + MF2)(–2a) = 4cx
=> MF1 + MF2 = = –x. Khi đó:
(MF1 + MF2) + (MF1 – MF2) = – + (–2a) => 2MF1 = –
=> MF1 =
(MF1 + MF2) – (MF1 – MF2) = – – (–2a) => 2MF2 = - + 2a
=> MF2 = a –c/a x.
c) Ta có: MF12 – MF22 = 4cx => (MF1 + MF2)(MF1 – MF2) = 4cx => (MF1 + MF2)2a = 4cx
=> MF1 + MF2 = = x. Khi đó:
(MF1 + MF2) + (MF1 – MF2) = + 2a => 2MF1 = + 2a
=> MF1 = a + x.
(MF1 + MF2) – (MF1 – MF2) = – 2a => 2MF2 = – 2a
=> MF2 = – a +x.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Hypebol có đáp án !!
Copyright © 2021 HOCTAP247
