Trang chủ
Đề thi & kiểm tra
Lớp 10
Toán học
Bài tập Chuyên đề Ba đường Conic có đáp án !!
Cho đường thẳng Δ và điểm O sao cho khoảng...
Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến delta là OH = 1 (Hình 39).
Câu hỏi :
Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).
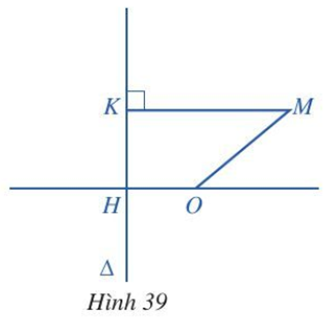
Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK2 – MO2 = 1 là một đường parabol.
Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).

Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK2 – MO2 = 1 là một đường parabol.
* Đáp án
* Hướng dẫn giải
Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.
Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).
Khi đó:
MK2 – MO2 = 1
{[x – (–1)]2 + (y – y)2} – [(0 – x)2 + (0 – y)2] = 1
{(x + 1)2 + 02} – [x2 + y2] = 1
(x2 + 2x +1) – (x2 + y2) = 1
2x +1 – y2 = 1
y2 = 2x.
Vậy tập hợp các điểm M là parabol có phương trình y2 = 2x.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Chuyên đề Ba đường Conic có đáp án !!
Số câu hỏi: 8
Copyright © 2021 HOCTAP247
