Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC (Hình 14).
Câu hỏi :
Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC (Hình 14).
a) Tìm các vectơ bằng vectơ
b) Tìm các vectơ đối của vectơ .
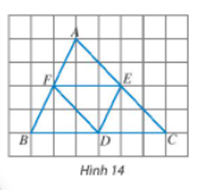
Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC (Hình 14).
a) Tìm các vectơ bằng vectơ
b) Tìm các vectơ đối của vectơ .

* Đáp án
* Hướng dẫn giải
a) Tam giác ABC có F và E lần lượt là trung điểm của AB và AC.
Do đó EF là đường trung bình của tam giác ABC nên EF // = BC.
Do D là trung điểm của BC nên BD = DC = .
Suy ra EF = BD = DC và EF // BD, EF // DC.
Hai vectơ và có giá song song với nhau, có cùng hướng đi từ phải qua trái nên hai vectơ này cùng hướng, hơn nữa .
Do đó .
Tương tự ta có: (do chúng cùng hướng và cùng độ dài).
b) Ta có FD là đường trung bình của tam giác ABC nên FD // = AC.
Mà E là trung điểm của AC nên AE = EC = .
Do đó: AE = EC = FD.
Hai vectơ và có giá song song và có hướng ngược nhau nên hai vectơ này ngược hướng. Hơn nữa .
Do đó và là hai vectơ đối nhau hay .
Hai vectơ và có giá trùng nhau và có hướng ngược nhau nên hai vectơ này ngược hướng. Hơn nữa .
Do đó và là hai vectơ đối nhau hay .
Ngoài ra, ta còn có .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Vectơ có đáp án !!
Copyright © 2021 HOCTAP247
