Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16).
Câu hỏi :
Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16).
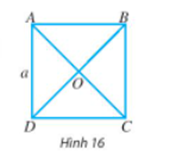
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng .
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng .
Cho hình vuông ABCD có tâm O và có cạnh bằng a (Hình 16).

a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng .
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng .
* Đáp án
* Hướng dẫn giải
Do ABCD là hình vuông nên tam giác ABD vuông cân tại A, theo định lí Pythagore, ta có: BD2 = AD2 + AB2 = a2 + a2 = 2a2
Suy ra: BD = .
Do đó: AC = BD = (hai đường chéo của hình vuông bằng nhau).
O là tâm của hình vuông ABCD nên O là giao điểm của hai đường chéo AC và BD, đồng thời là trung điểm của mỗi đường.
Do đó: AO = OC = ; BO = OD = .
a) Hai vectơ và cùng phương và cùng hướng, hơn nữa , , nên .
Do đó: và .
Ngoài ra, có thể tìm được các cặp vectơ bằng nhau và có độ dài bằng khác như sau:
+) và .
+) và .
+) và .
b) Trong hình đã cho chỉ có hai cạnh AC và BD là bằng nhau và bằng . Tuy nhiên hai cạnh này cắt nhau nên hai vectơ và không cùng phương nên chúng không đối nhau.
Vậy không có hai vectơ thỏa mãn yêu cầu bài toán.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Vectơ có đáp án !!
Copyright © 2021 HOCTAP247
