Cho hình thang ABCD có hai đáy là AB và DC. Cho biết vecto a = vecto AC + vecto CB, vecto b = vecto DB + vecto BC . Chứng minh hai vectơ

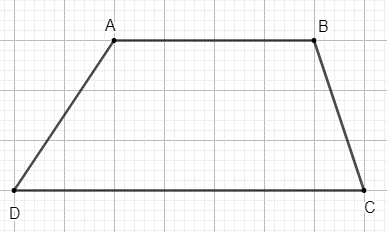
Vì ABCD là hình thang với AB và DC là hai đáy nên AB // DC.

Do đó hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng phương, hơn nữa chúng cùng hướng đi từ trái qua phải.

Nên hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{DC}$ cùng hướng.

Theo quy tắc ba điểm ta có:

$\overrightarrow{a}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$

$\overrightarrow{b}=\overrightarrow{DB}+\overrightarrow{BC}=\overrightarrow{DC}$

Vậy hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng hướng.