Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

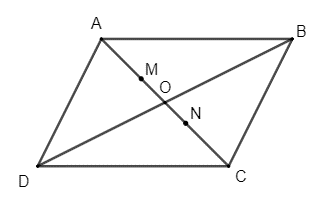
a) Gọi M là trọng tâm tam giác ADB.

Khi đó ta có: $\overrightarrow{MA}+\overrightarrow{MD}+\overrightarrow{MB}=\overrightarrow{0}$.

Vậy điểm M thỏa mãn $\overrightarrow{MA}+\overrightarrow{MD}+\overrightarrow{MB}=\overrightarrow{0}$ là trọng tâm của tam giác ADB.

b) Tương tự câu a, điểm N thỏa mãn $\overrightarrow{ND}+\overrightarrow{NB}+\overrightarrow{NC}=\overrightarrow{0}$ là trọng tâm của tam giác DBC.

c) ABCD là hình bình hành có tâm O nên O là giao của hai đường chéo AC và BD, đồng thời là trung điểm của mỗi đường.

Khi đó AO là đường trung tuyến của tam giác ABD nên trọng tâm M của tam giác này nằm trên cạnh AO thỏa mãn AM = $\frac{2}{3}$AO nên OM = $\frac{1}{3}$AO.

Và CO là đường trung tuyến của tam giác BDC nên trọng tâm N của tam giác này nằm trên cạnh CO thỏa mãn CN = $\frac{2}{3}$CO nên ON = $\frac{1}{3}$CO.

Mà AO = CO.

Do đó: ON = OM.

Và O, M, N thẳng hàng (cùng thuộc đường chéo AC).

Nên O là trung điểm của MN.

Suy ra $\overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{0}$.

Mà $\overrightarrow{PM}+\overrightarrow{PN}=\overrightarrow{0}$ nên điểm P trùng với điểm O.

Vậy điểm P thỏa mãn $\overrightarrow{PM}+\overrightarrow{PN}=\overrightarrow{0}$ là tâm O của hình bình hành ABCD.