Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: vecto KA + vecto KC = 0

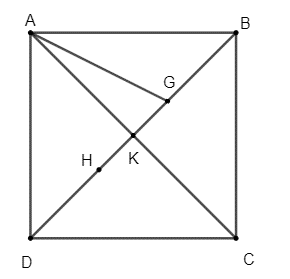
Vì K là điểm thỏa mãn $\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{0}$ nên K là trung điểm của AC.

Vì G là điểm thỏa mãn $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ nên G là trọng tâm của tam giác ABC.

Vì H là điểm thỏa mãn $\overrightarrow{HA}+\overrightarrow{HD}+\overrightarrow{HC}=\overrightarrow{0}$ nên H là trọng tâm của tam giác ADC.

Do ABCD là hình vuông nên hai đường chéo AC, BD bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên K cũng là trung điểm của BD hay K chính là tâm của hình vuông ABCD.

Trong tam giác ABC, có BK là đường trung tuyến nên G ∈ BK và $GK=\frac{1}{3}BK$ (suy ra từ tính chất trọng tâm tam giác).

Trong tam giác ADC, có DK là đường trung tuyến nên H ∈ DK và $HK=\frac{1}{3}DK$ (suy ra từ tính chất trọng tâm tam giác).

Suy ra H, K, G thẳng hàng và cùng thuộc DB.

Hình vuông ABCD cạnh a nên AC = BD = $a\sqrt{2}$.

Khi đó: AK = KC = DK = KB = $\frac{1}{2}$AC = $\frac{1}{2}$BD = $\frac{a\sqrt{2}}{2}$.