a) Ta có: $\vec{M B} = \frac{1}{2} \vec{B C}$ nên ba điểm M, B, C thẳng hàng và vectơ $\vec{M B}$ cùng hướng với vectơ $\vec{B C}$ sao cho $| \vec{M B} | = \frac{1}{2} . | \vec{B C} |$ hay MB = $\frac{1}{2}$ BC.

Lại có: $\vec{A N} = 3 \vec{N B}$ nên ba điểm A, N, B thẳng hàng và vectơ $\vec{A N}$ cùng hướng với vectơ $\vec{N B}$ sao cho $| \vec{A N} | = 3 | \vec{N B} |$ hay AN = 3NB.

Có:

$\vec{C P} = \vec{P A}$ $\Leftrightarrow \vec{P A} - \vec{C P} = \vec{0} \Leftrightarrow \vec{P A} + (- \vec{C P}) = \vec{0}$ $\Leftrightarrow \vec{P A} + \vec{P C} = \vec{0}$

⇔ P là trung điểm của đoạn thẳng AC.

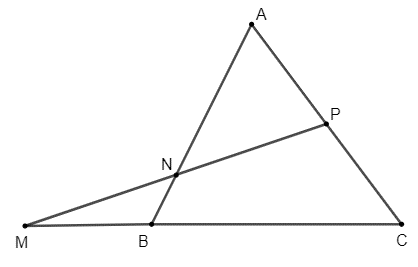
Media VietJack

b) Vì AN = 3NB nên BN = $\frac{1}{4}$ BA, do đó: $\vec{B N} = \frac{1}{4} \vec{B A}$ .

Ta có: $\vec{M N} = \vec{M B} + \vec{B N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$ .

Vì MB = $\frac{1}{2}$ BC nên $M C = \frac{3}{2} B C$ , do đó: $\vec{M C} = \frac{3}{2} \vec{B C}$ .

P là trung điểm của AC nên $\vec{C P} = \frac{1}{2} \vec{C A}$ .

Nên ta có: $\vec{M P} = \vec{M C} + \vec{C P} = \frac{3}{2} \vec{B C} + \frac{1}{2} \vec{C A}$

$= (\frac{3}{2} - \frac{1}{2}) \vec{B C} + \frac{1}{2} \vec{B A} = \vec{B C} + \frac{1}{2} \vec{B A}$ .

Vậy $\vec{M N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$ và $\vec{M P} = \vec{B C} + \frac{1}{2} \vec{B A}$ .

c) Theo câu b ta có:

$\vec{M N} = \frac{1}{2} \vec{B C} + \frac{1}{4} \vec{B A}$ $= \frac{1}{2} (\vec{B C} + \frac{1}{2} \vec{B A}) = \frac{1}{2} \vec{M P}$ .

Do đó: $\vec{M N} = \frac{1}{2} \vec{M P}$ .

Từ đó suy ra ba điểm M, N, P thẳng hàng.

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Cho tam giác ABC. a) Xác định các điểm M, N, P thỏa mãn:

Câu hỏi :

Cho tam giác ABC. a) Xác định các điểm M, N, P thỏa mãn: MB→=12BC→, AN→=3NB→, CP→=PA→. b) Biểu thị mỗi vectơ MN→, MP→ theo hai vectơ BC→, BA→. c) Chứng minh ba điểm M, N, P thẳng hàng.

* Đáp án

* Hướng dẫn giải

Bài tập Tích của một số với một vectơ có đáp án !!