Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

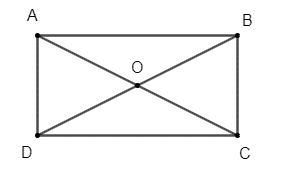
Vì ABCD là hình chữ nhật nên BC = AD = a, CD = AB = 2a, hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.

Áp dụng định lí Pythagore cho tam giác vuông ABC ta có:

AC² = AB² + BC² = (2a)² + a² = 5a² $\Rightarrow AC=a\sqrt{5}$ .

Do đó: $BD=AC=a\sqrt{5}$ .

Suy ra: $AO=\frac{1}{2}AC=\frac{1}{2}.a\sqrt{5}=\frac{a\sqrt{5}}{2}$ .

Ta có: $\text{co}s\widehat{BAO}\text{\hspace{0.17em}=\hspace{0.17em}co}s\widehat{BAC}=\frac{AB}{AC}=\frac{2a}{a\sqrt{5}}=\frac{2}{\sqrt{5}}$ .

a) $\overrightarrow{AB}.\overrightarrow{AO}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AO}\right|.cos(\overrightarrow{AB},\overrightarrow{AO})$$=AB.AO.\cos \widehat{BAO}$$=2a.\frac{a\sqrt{5}}{2}.\frac{2}{\sqrt{5}}=2a^2$ .

b) $\overrightarrow{AB}.\overrightarrow{AD}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AD}\right|.cos(\overrightarrow{AB},\overrightarrow{AD})$$=AB.AD.cos\widehat{BAD}$  = 2a . a . cos90° = 0.