Biểu thức F = y – x đạt giá trị nhỏ nhất với điều kiện

* Hướng dẫn giải

Đáp án đúng là: A

Biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{c}-2x+y\le -2\\ x-2y\le 2\\ x+y\le 5\\ x\ge 0\end{array}\right.$ trên hệ trục tọa độ

Ta vẽ đường thẳng d₁: – 2x + y = – 2, đường thẳng d₁ đi qua hai điểm (0; – 2) và (1; 0)

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có – 2.0 + 0 = 0 > – 2, điểm O(0; 0) không thoả mãn bất phương trình – 2x + y ≤ – 2, vậy điểm O(0; 0) không thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d₁ và không chứa điểm O(0; 0) (kể cả bờ).

Ta vẽ đường thẳng d₂: x – 2y = 2, đường thẳng d₂ đi qua hai điểm (0; – 1) và (2; 0)

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 – 2.0 = 0 < 2, điểm O(0; 0) thoả mãn bất phương trình x – 2y ≤ 2, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d₂ và chứa điểm O(0; 0) (kể cả bờ).

Ta vẽ đường thẳng d₃: x + y = 5, đường thẳng d₃ đi qua hai điểm (0; 5) và (5; 0)

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 + 0 = 0 < 5, điểm O(0; 0) thoả mãn bất phương trình x + y ≤ 5, vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Ta có miền nghiệm của bất phương trình là phần nửa mặt phẳng được chia bởi d₃ và chứa điểm O(0; 0) (kể cả bờ).

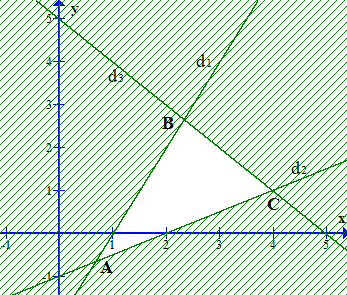
Miền nghiệm là phần không bị gạch trong hình dưới đây (kể cả bờ).