a) Dựa vào đồ thị của hàm số y =1/2x^2 (H.6.2), tìm x sao cho y = 8. b) Vẽ đồ thị của các hàm số y = 2x + 1 và y = 2x2 trên cùng một mặt phẳng tọa độ.

Hướng dẫn giải

a) Với y = 8, từ điểm 8 trên trục Oy, ta kẻ đường thẳng song song với Ox, đường thẳng này cắt đồ thị hàm số \(y = \frac{1}{2}{x^2}\) tại hai điểm, từ hai điểm đó hạ vuông góc xuống trục Ox, ta thấy hai chân đường vuông góc trên Ox là điểm 4 và – 4.

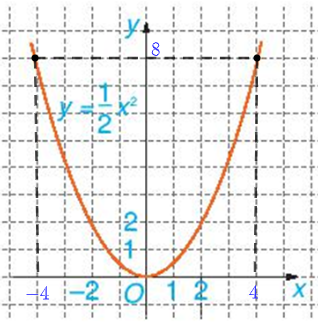
Vậy với y = 8 thì x = 4, x = – 4.

b)

+ Ta có: y = 2x + 1

Tập xác định của hàm số là \(\mathbb{R}\).

Với x = 0 thì y = 2 . 0 + 1 = 1.

Với x = 1 thì y = 2 . 1 + 1 = 3.

Do đó đồ thị hàm số y = 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; 3).

+ Ta có: y = 2x²

Tập xác định của hàm số là \(\mathbb{R}\).

Bảng giá trị tương ứng của x và y

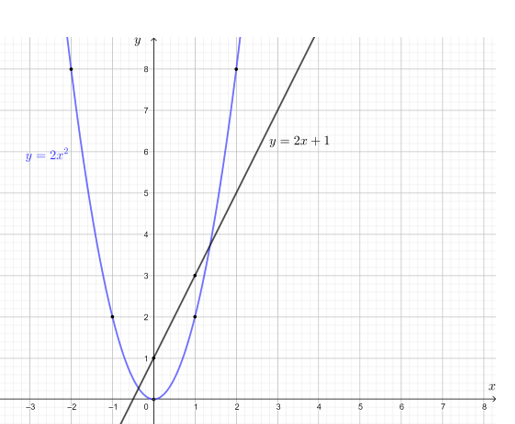
Trên mặt phẳng tọa độ, lấy các điểm (0; 0), (1; 2), (– 1; 2), (2; 8), (– 2; 8) rồi lần lượt nối chúng để được đường cong là đồ thị của hàm số y = 2x².