Vẽ parabol y = 3x2 – 10x + 7. Từ đó tìm khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số y = 3x2 – 10x + 7.

Hướng dẫn giải

Ta có: a = 3 > 0 nên parabol quay bề lõm lên trên.

Parabol y = 3x² – 10x + 7 có:

+ Tọa độ đỉnh I\(\left( {\frac{5}{3}; - \frac{4}{3}} \right)\);

+ Trục đối xứng \(x = \frac{5}{3}\);

+ Giao điểm của đồ thị với trục Oy là A(0; 7).

+ Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình 3x² – 10x + 7 = 0, tức là x = \(\frac{7}{3}\) và x = 1;

+ Điểm đối xứng với điểm A qua trục đối xứng \(x = \frac{5}{3}\) là B\(\left( {\frac{{10}}{3};7} \right)\).

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.

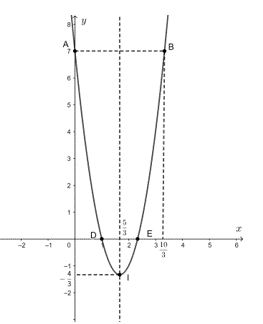
Quan sát đồ thị, ta thấy:

+ Đồ thị hàm số đi xuống từ trái qua phải trên khoảng \(\left( { - \infty ;\frac{5}{3}} \right)\) nên hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{5}{3}} \right)\).

+ Đồ thị hàm số đi lên từ trái qua phải trên khoảng \(\left( {\frac{5}{3}; + \infty } \right)\) nên hàm số đồng biến trên khoảng \(\left( {\frac{5}{3}; + \infty } \right)\).

+ Điểm thấp nhất của đồ thị là đỉnh I\(\left( {\frac{5}{3}; - \frac{4}{3}} \right)\), vậy giá trị nhỏ nhất của hàm số là \(y = - \frac{4}{3}\), khi \(x = \frac{5}{3}\).