Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng rau. a) Tính diện tích mảnh vườn hình chữ nhật được rào theo chiều rộng x (mét) của nó.

Hướng dẫn giải

a) Bác Hùng dùng lưới để rào thành một mảnh vườn hình chữ nhật có chiều rộng x (mét) như sau:

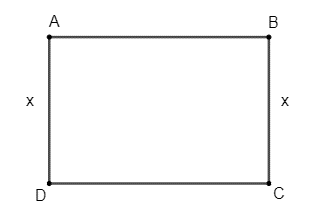
Vì tấm lưới dài 40 m, hay chính là chu vi của mảnh vườn hình chữ nhật ABCD là 40 m.

Suy ra nửa chu vi của mảnh vườn là 40 : 2 = 20 m.

Do đó chiều dài của mảnh vườn rào được theo chiều rộng x (mét) là: 20 – x (m).

Diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng x (mét) là:

S(x) = x . (20 – x) = – x² + 20x (m²).

b) Để tìm diện tích lớn nhất của mảnh vườn hình chữ nhật bác Hùng có thể rào được, ta tính giá trị lớn nhất của hàm số S(x), đây là hàm số bậc hai.

Tọa độ đỉnh của đồ thị hàm số bậc hai S(x) = – x² + 20x là I(10; 100).

Do đó giá trị lớn nhất của hàm số S(x) là S =100 tại x = 10.

Suy ra chiều dài khi chiều rộng x = 10 m là 20 – 10 = 10 (m).

Vậy để mảnh vườn rào được có diện tích lớn nhất thì bác Hùng nên rào lưới thép gai thành hình vuông có độ dài cạnh là 10 m.