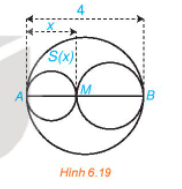
Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) diện tích phần hình phẳng nằm trong...
Câu hỏi :
Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
Vì AM = x nên x > 0, lại có AM < AB nên x < 4, vậy điều kiện của x là 0 < x < 4.
Đường tròn lớn có đường kính AB = 4 nên bán kính của hình tròn này là R = 2.
Diện tích hình tròn lớn này là SR = πR2 = π . 22 = 4π.
Đường tròn nhỏ đường kính AM = x có bán kính là r1 = \(\frac{x}{2}\).
Diện tích hình tròn nhỏ có bán kính r1 là S1 = πr12 = π . \({\left( {\frac{x}{2}} \right)^2} = \frac{{{x^2}}}{4}\pi \).
Ta có: AM + MB = AB ⇒ MB = AB – AM = 4 – x.
Đường tròn đường kính MB có bán kính là r2 = \(\frac{{4 - x}}{2}\).
Diện tích hình tròn có bán kính r2 là S2 = πr22 = \(\pi .{\left( {\frac{{4 - x}}{2}} \right)^2} = \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi \).
Tổng diện tích hai hình tròn nhỏ là:
S12 = S1 + S2 = \(\frac{{{x^2}}}{4}\pi + \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi \) = \(\frac{{{x^2} + {{\left( {4 - x} \right)}^2}}}{4}\pi \)\( = \frac{{{x^2} - 4x + 8}}{2}\pi \).
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là
S(x) = SR – S12 = \(4\pi - \frac{{{x^2} - 4x + 8}}{2}\pi \)\( = \frac{{ - {x^2} + 4x}}{2}\pi \).
Vì diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ hay diện tích S(x) nhỏ hơn hoặc bằng nửa tổng diện tích hia hình tròn nhỏ hay S(x) ≤ \(\frac{1}{2}{S_{12}}\).
Khi đó: \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
⇔ – 2x2 + 8x ≤ x2 – 4x + 8
⇔ 3x2 – 12x + 8 ≥ 0
Xét tam thức f(x) = 3x2 – 12x + 8 có ∆' = (– 6)2 – 3 . 8 = 12 > 0 nên f(x) có hai nghiệm x1 = \(\frac{{6 - \sqrt {12} }}{3} = \frac{{6 - 2\sqrt 3 }}{3}\) và x2 = \(\frac{{6 + \sqrt {12} }}{3} = \frac{{6 + 2\sqrt 3 }}{3}\).
Mặt khác hệ số a = 3 > 0, do đó ta có bảng xét dấu f(x):
|
x |
– ∞ \(\frac{{6 - 2\sqrt 3 }}{3}\) \(\frac{{6 + 2\sqrt 3 }}{3}\) + ∞ |
|
f(x) |
+ 0 – 0 + |
Do đó f(x) ≥ 0 với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\).
Kết hợp với điều kiện 0 < x < 4.
Vậy các giá trị của x thỏa mãn yêu cầu của đề bài là \(x \in \left( {0;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3};4} \right)\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 17. Dấu của tam thức bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
