Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp x...
Câu hỏi :
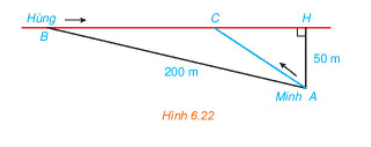
Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B, cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ của Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường (H.6.22) để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười).

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
Đổi: 200 m = 0,2 km, 50 m = 0,05 km.
Đặt CH = x (km) (x > 0).
Xét tam giác CHA vuông tại H, theo định lí Pythagore ta có:
CA2 = HA2 + HC2 = (0,05)2 + x2 = 0,0025 + x2
Suy ra CA = \(\sqrt {0,0025 + {x^2}} \) hay quãng đường di chuyển của Minh từ vị trí A đến điểm gặp nhau C dài \(\sqrt {0,0025 + {x^2}} \) km.
Vận tốc đi bộ của Minh là 5 km/h nên thời gian di chuyển của Minh từ vị trí A đến điểm gặp nhau C là: \(\frac{{\sqrt {0,0025 + {x^2}} }}{5}\) (giờ).
Xét tam giác HAB vuông tại H, theo định lí Pythagore ta có:
AB2 = HB2 + HA2 ⇔ HB2 = AB2 – HA2 = (0,2)2 – (0,05)2 = 0,0375
Suy ra HB = \(\frac{{\sqrt {15} }}{{20}}\).
Ta có: BC + CH = HB ⇔ BC = HB – CH = \(\frac{{\sqrt {15} }}{{20}} - x\).
Do đó quãng đường di chuyển của Hùng từ B đến điểm gặp nhau C dài \(\frac{{\sqrt {15} }}{{20}} - x\) km.
Vận tốc đạp xe của Hùng là 15 km/h nên thời gian di chuyển của Hùng từ B đến điểm gặp nhau là: \(\frac{{\frac{{\sqrt {15} }}{{20}} - x}}{{15}} = \frac{{\sqrt {15} - 20x}}{{300}}\) (giờ).
Để hai bạn gặp nhau mà không bạn nào phải chờ người kia thì thời gian di chuyển từ vị trí A đến C của Minh phải bằng thời gian di chuyển từ vị trí B đến C của Hùng.
Khi đó ta có phương trình: \(\frac{{\sqrt {0,0025 + {x^2}} }}{5} = \frac{{\sqrt {15} - 20x}}{{300}}\) (1).
Giải phương trình (1) ta có:
(1) \( \Leftrightarrow 60\sqrt {0,0025 + {x^2}} = \sqrt {15} - 20x\)
Bình phương hai vế của phương trình trên ta được:
3600.(0,0025 + x2) = 15 – 40\(\sqrt {15} \)x + 400x2
⇔ 3200x2 + 40\(\sqrt {15} \)x – 6 = 0
⇔ x = \(\frac{{ - \sqrt {15} - 3\sqrt 7 }}{{160}}\) hoặc x = \(\frac{{ - \sqrt {15} + 3\sqrt 7 }}{{160}}\)
Thay lần lượt các giá trị này vào phương trình (1) ta thấy cả hai giá trị đều thỏa mãn.
Lại có điều kiện của x là x > 0 nên ta chọn x = \(\frac{{ - \sqrt {15} + 3\sqrt 7 }}{{160}}\)≈ 0,0254.
Suy ra BC = BH – CH ≈ \(\frac{{\sqrt {15} }}{{20}} - 0,0254 \approx 0,1682\) km = 168,2 m.
Vậy vị trí C thỏa mãn yêu cầu đề bài là điểm cách B khoảng 168,2 m.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 18. Phương trình quy về phương trình bậc hai có đáp án !!
Copyright © 2021 HOCTAP247
