Cho hai đường thẳng cắt nhau ∆1, ∆2 tương ứng có các vectơ pháp tuyến vecto n1, vecto n2. Gọi φ là góc giữa hai đường thẳng đó (H.7.7). Nêu mối quan hệ giữa:
Câu hỏi :
Cho hai đường thẳng cắt nhau ∆1, ∆2 tương ứng có các vectơ pháp tuyến \({\overrightarrow n _1},\,\,{\overrightarrow n _2}\). Gọi φ là góc giữa hai đường thẳng đó (H.7.7). Nêu mối quan hệ giữa:
a) góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\);
b) cosφ và cos\(\left( {{{\overrightarrow n }_1},\,{{\overrightarrow n }_2}} \right)\).
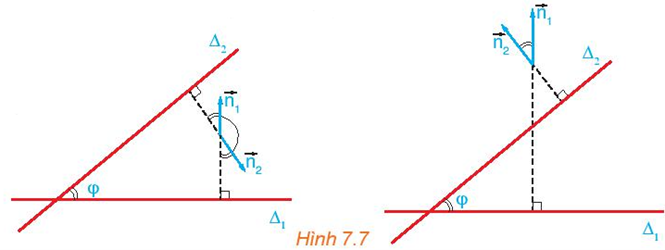
Cho hai đường thẳng cắt nhau ∆1, ∆2 tương ứng có các vectơ pháp tuyến \({\overrightarrow n _1},\,\,{\overrightarrow n _2}\). Gọi φ là góc giữa hai đường thẳng đó (H.7.7). Nêu mối quan hệ giữa:
a) góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\);
b) cosφ và cos\(\left( {{{\overrightarrow n }_1},\,{{\overrightarrow n }_2}} \right)\).

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
a) Quan sát Hình 7.7, ta thấy góc giữa hai đường thẳng ∆1 và ∆2 là góc φ, góc này bằng hoặc bù với góc giữa hai vectơ \({\overrightarrow n _1}\) và \({\overrightarrow n _2}\).
b)
+) Với trường hợp góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\) bằng nhau thì ta có: cosφ = cos\(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\);
+) Với trường hợp góc φ và góc \(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\) bù nhau thì ta có: cosφ = – cos\(\left( {{{\overrightarrow n }_1},\,\,{{\overrightarrow n }_2}} \right)\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 20. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án !!
Copyright © 2021 HOCTAP247
