Cho đường thẳng ∆: y = ax + b với a ≠ 0. a) Chứng minh rằng ∆ cắt trục hoành. b) Lập phương trình đường thẳng ∆0 đi qua O(0; 0) và song song (hoặc trùng) với ∆. c) Hãy chỉ ra mối q...
Câu hỏi :
Cho đường thẳng ∆: y = ax + b với a ≠ 0.
a) Chứng minh rằng ∆ cắt trục hoành.
b) Lập phương trình đường thẳng ∆0 đi qua O(0; 0) và song song (hoặc trùng) với ∆.
c) Hãy chỉ ra mối quan hệ giữa α∆ và α∆0.
d) Gọi M là giao điểm của ∆0 với nửa đường tròn đơn vị và x0 là hoành độ của M. Tính tung độ của M theo x0 và a. Từ đó, chứng minh rằng tanα∆ = a.
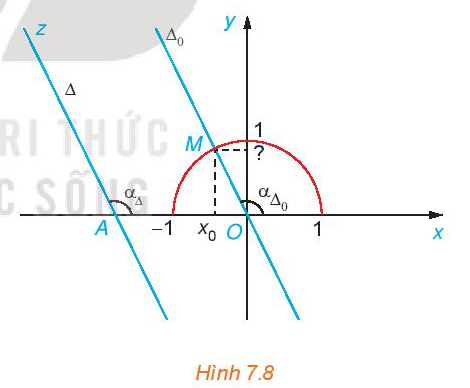
Cho đường thẳng ∆: y = ax + b với a ≠ 0.
a) Chứng minh rằng ∆ cắt trục hoành.
b) Lập phương trình đường thẳng ∆0 đi qua O(0; 0) và song song (hoặc trùng) với ∆.
c) Hãy chỉ ra mối quan hệ giữa α∆ và α∆0.
d) Gọi M là giao điểm của ∆0 với nửa đường tròn đơn vị và x0 là hoành độ của M. Tính tung độ của M theo x0 và a. Từ đó, chứng minh rằng tanα∆ = a.

* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
a) Phương trình trục hoành Ox: y = 0.
Xét hệ \(\left\{ \begin{array}{l}y = 0\\y = ax + b\end{array} \right.\).
Khi đó ta có: ax + b = 0 ⇔ x = \( - \frac{b}{a}\) (do a ≠ 0).
Do đó hệ trên có nghiệm duy nhất \(\left( { - \frac{b}{a};\,0} \right)\) nên ∆ và trục hoành cắt nhau tại giao điểm có tọa độ \(\left( { - \frac{b}{a};\,0} \right)\).
b) Đường thẳng ∆ có vectơ pháp tuyến là \(\overrightarrow n = \left( {a;\,\, - 1} \right)\).
Do đường thẳng ∆0 song song hoặc trùng với ∆ nên ta chọn vectơ \(\overrightarrow n \) là một vectơ pháp tuyến của ∆0.
Đường thẳng ∆0 đi qua điểm O(0; 0) và nhận \(\overrightarrow n = \left( {a;\,\, - 1} \right)\) làm vectơ pháp tuyến.
Khi đó phương trình đường thẳng ∆0 là: a(x – 0) – (y – 0) = 0 hay ax – y = 0 hay y = ax.
c) Khi ∆ và ∆0 trùng nhau thì α∆ và α∆0 trùng nhau nên α∆ = α∆0.
Khi ∆ và ∆0 song song thì α∆ = α∆0 (do hai góc ở vị trí đồng vị).
Vậy α∆ = α∆0.
d) Vì M thuộc đường thẳng ∆0 nên tọa độ điểm M thỏa mãn phương trình đường thẳng ∆0 nên khi có hoành độ x0 thì tung độ của M là y0 = ax0.
Ta có tanα∆0 = tan\(\widehat {xOM}\) = \(\frac{{{y_0}}}{{{x_0}}} = \frac{{a{x_0}}}{{{x_0}}} = a\) (theo định nghĩa giá trị lượng giác)
Do α∆ = α∆0 nên tanα∆ = tanα∆0 = a.
Vậy tanα∆ = a.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 20. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án !!
Copyright © 2021 HOCTAP247
