Viết phương trình đường tròn (C) đi qua ba điểm M(4; – 5), N(2; – 1), P(3; – 8).
Câu hỏi :
Viết phương trình đường tròn (C) đi qua ba điểm M(4; – 5), N(2; – 1), P(3; – 8).
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
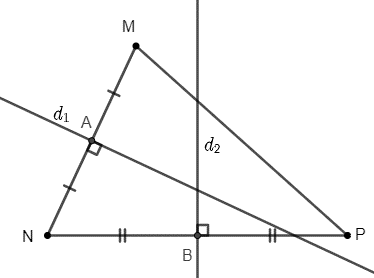
Các đoạn thẳng MN, NP tương ứng có trung điểm là A(3; – 3), B\(\left( {\frac{5}{2};\,\,\frac{{ - 9}}{2}} \right)\). Đường thẳng trung trực d1 của đoạn thẳng MN đi qua điểm A(3; – 3) và có vectơ pháp tuyến \(\overrightarrow {MN} = \left( { - 2;\,4} \right)\).
Vì \(\overrightarrow {MN} = \left( { - 2;4} \right)\) cùng phương với \(\overrightarrow {{n_1}} = \left( {1;\, - 2} \right)\) nên d1 cũng nhận \(\overrightarrow {{n_1}} = \left( {1;\, - 2} \right)\) là vectơ pháp tuyến. Do đó, phương trình của d1 là: 1(x – 3) – 2(y + 3) = 0 hay x – 2y – 9 = 0.
Đường thẳng trung trực d2 của đoạn thẳng NP đi qua B\(\left( {\frac{5}{2};\,\,\frac{{ - 9}}{2}} \right)\) và có vectơ pháp tuyến \(\overrightarrow {NP} = \left( {1;\, - 7} \right)\), do đó phương trình d2 là: \(1\left( {x - \frac{5}{2}} \right) - 7\left( {y + \frac{9}{2}} \right) = 0\) hay x – 7y – 34 = 0.
Tâm I của đường tròn (C) cách đều ba điểm M, N, P nên I là giao điểm của d1 và d2.
Vậy tọa độ của I là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 2y - 9 = 0\\x - 7y - 34 = 0\end{array} \right.\).
Suy ra I(– 1; – 5). Đường tròn (C) có bán kính là IM =\(\sqrt {{{\left( {4 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 5 - \left( { - 5} \right)} \right)}^2}} = 5\).
Vậy phương trình của (C) là: (x + 1)2 + (y + 5)2 = 25.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập Bài 21. Đường tròn trong mặt phẳng tọa độ có đáp án !!
Copyright © 2021 HOCTAP247
